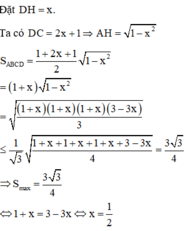Các câu hỏi tương tự
Cho hình thang cân ABCD có đáy nhỏ AB. Biết AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất của hình thang. A.
8
2
9
B.
4
2
9
C.
3
3
2
D.
3
3...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB. Biết AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất của hình thang.
A. 8 2 9
B. 4 2 9
C. 3 3 2
D. 3 3 4
Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất
S
m
a
x
của hình thang A.
S
m
a
x
8
2
9
B.
S
m
a...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất S m a x của hình thang
A. S m a x = 8 2 9
B. S m a x = 4 2 9
C. S m a x = 3 3 2
D. S m a x = 3 3 4
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0xa). Mặt phẳng
(
α
)
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x
a
3
C.
x
a...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x
0
x
α
. Mặt phẳng
α
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x 0 < x < α . Mặt phẳng α qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A, B, D). sao cho
A
B
A
M
+
2.
A
D
A
N
4.
Kí hiệu V,
V
1
lần lượt là thể tích của các khối chóp...
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành. Hai điểm M, N thuộc các cạnh AB và AD (M, N không trùng với A, B, D). sao cho A B A M + 2. A D A N = 4. Kí hiệu V, V 1 lần lượt là thể tích của các khối chóp S . A B C D v à S . M B C D N . Tìm giá trị lớn nhất của V 1 V
A. 2 3
B. 3 4
C. 1 6
D. 14 17
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AD//BC), BC2a, ABADDCa với a0. Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và BD. Biết SD vuông góc AC. M là một điểm thuộc đoạn OD; MDx với x0; M khác O và D. Mặt phẳng (α) đi qua (α) đi qua M và song song với hai đường thẳng SD và AC cắt khối chóp S.ABCD theo một thiết diện. Tìm x để diện tích thiết diện là lớn nhất? A.
a
3
4
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân (AD//BC), BC=2a, AB=AD=DC=a với a>0. Mặt bên SBC là tam giác đều. Gọi O là giao điểm của AC và BD. Biết SD vuông góc AC. M là một điểm thuộc đoạn OD; MD=x với x>0; M khác O và D. Mặt phẳng (α) đi qua (α) đi qua M và song song với hai đường thẳng SD và AC cắt khối chóp S.ABCD theo một thiết diện. Tìm x để diện tích thiết diện là lớn nhất?
A. a 3 4
B. a 3
C. a 3 2
D. a
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2
9
điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ...
Đọc tiếp
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9 điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là
A. ( P ) : x + 2 y + 3 z + 6 = 0
B. ( P ) : x + 2 y + z - 2 = 0
C. ( P ) : x - 2 y + z - 6 = 0
D. ( P ) : 3 x + 2 y + 2 z - 4 = 0
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân. A. D ( 4;3;0 ) B. D
164
49
;
51
49
;
48
49
C. D
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Cho hình chóp S.ABCD có đáy BACD là hình vuông cạnh a, cạnh bên SA a và vuông góc với mặt đáy (ABCD). Trên SB, SD lần lượt lấy hai điểm M, N sao cho
S
M
S
B
m
0
,
S
N
S
D
n
0
.
Tính thể tích lớn nhất...
Đọc tiếp
Cho hình chóp S.ABCD có đáy BACD là hình vuông cạnh a, cạnh bên SA = a và vuông góc với mặt đáy (ABCD). Trên SB, SD lần lượt lấy hai điểm M, N sao cho S M S B = m > 0 , S N S D = n > 0 . Tính thể tích lớn nhất V max của khối chóp S,AMN biết 2 m 2 + 3 n 2 = 1 .
A. V max = a 3 6 72
B. V max = a 3 48
C. V max = a 3 3 24
D. V max = a 3 6