Đáp án C
Độ dài đường sinh là: 2.2 = 4 (cm)
Độ dài đường cao là:
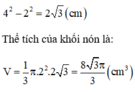
Đáp án C
Độ dài đường sinh là: 2.2 = 4 (cm)
Độ dài đường cao là:
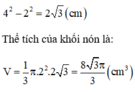
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h = 3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P = R + 2r.
A. 2 3
B. 3
C. 3 3
D. 2
Cho hình nón có thể tích bằng 12 π và diện tích xung quanh bằng 15. Tính bán kính đáy của hình nón biết bán kính là số nguyên dương.
A. 4
B. 3.
C. 6
D. 5
Một khối nón có bán kính đáy bằng 3 và góc ở đỉnh bằng 60 ° thì có thể tích bằng bao nhiêu?
A. 9 π 3
B. 27 π 3
C. 3 π 3
D. 6 π 3
Cho hình nón (N) có đường cao SO=h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt O M = x , 0 < x < h . C là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
A. h/2
B. h 2 2
C. h 3 2
D. h/3
Cho hình nón có bán kính đáy bằng 2 cm, góc ở đỉnh bằng 60 ° . Thể tích của khối nón là
A. 8 3 π 9 c m 3
B. 8 3 π c m 3
C. 8 3 π 3 c m 3
D. 8 3 9 c m 3
Cho hình nón tròn xoay có bán kính đáy bằng 3 và diện tích xung quanh bằng 6 3 π . Góc ở đỉnh của hình nón đã cho bằng
A. 60 °
B. 150 °
C. 90 °
D. 120 °
Cho hình nón tròn xoay có bán kính đáy bằng 3 và diện tích xung quanh bằng 6 3 π . Góc ở đỉnh của hình nón đã cho bằng
A. 60 °
B. 150 °
C. 90 °
D. 120 °
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x (0 < x < h). (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Giá trị x theo h để thể tích khối nón đỉnh O đáy là (C) lớn nhất là:
A. x = h 2
B. x = h 2 2
C. x = h 3 2
D. x = h 3
Cho hình nón đỉnh S, chiều cao SO=h, bán kính đáy bằng R. Gọi M là điểm nằm trên đoạn SO , đặtOM=x (0<x<h) Cắt hình nón bằng mặt phẳng (P) đi qua M và vuông góc với SO, thiết diện thu được là đường tròn (C). Tìm x để thể tích của khối nón đỉnh O đáy là hình tròn giới hạn bởi (C) đạt giá trị lớn nhất
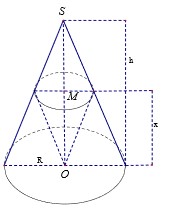
A. x = h 2
B. x = h 3
C. x = h 4
D. x = h 5