Các câu hỏi tương tự
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a, gọi
α
là góc giữa đường thẳng
A
B
và mặt phẳng
B
B
D
D
. Tính
sin
α
A.
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α
A. 3 5
B. 3 2
C. 1 2
D. 3 4
Cho hình hộp đứng ABCD.ABCD có đáy là hình thoi, tam giác ABD đều. Gọi M và N lần lượt là trung điểm BC và CD, biết rằng MN
⊥
BD. Gọi
α
là góc tạo bởi đường thẳng MN và mặt đáy (ABCD), khi đó giá trị cos
α
bằng A.
cos
α
1
3
B. ...
Đọc tiếp
Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình thoi, tam giác ABD đều. Gọi M và N lần lượt là trung điểm BC và C'D', biết rằng MN ⊥ B'D. Gọi α là góc tạo bởi đường thẳng MN và mặt đáy (ABCD), khi đó giá trị cos α bằng
A. cos α = 1 3
B. cos α = 3 2
C. cos α = 1 10
D. cos α = 1 2
Cho hình lập phương ABCD.ABCD có cạnh bên bằng a (tham khảo hình vẽ bên). Gọi
α
là góc giữa đường thẳng AC và mặt phẳng (ABCD) thì:
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bên bằng a (tham khảo hình vẽ bên). Gọi α là góc giữa đường thẳng A'C và mặt phẳng (A'B'C'D') thì:
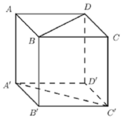
![]()

![]()
![]()
Cho hình lập phương ABCD.ABCD có cạnh bằng
3
. Mặt phẳng
α
cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng
α
biết
α
tạo với mặt (ABBA) một góc
60
0
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 . Mặt phẳng α cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng α biết α tạo với mặt (ABB'A') một góc 60 0 .
![]()
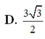
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi ( α ) là mặt phẳng đi qua A sao cho góc giữa OA và ( α ) bằng 30 ° . Đường thẳng đi qua A vuông góc với mặt phẳng ( α ) cắt mặt cầu tại B. Tính độ dài đoạn AB.
Cho hình hộp chữ nhật ABCD.ABCD có đáy là hình chữ nhật , AB a, AD 2, hình chiếu vuông góc của điểm A trên mặt phẳng
(
A
B
C
D
)
là trung điểm H của A’D’. Biết rằng AA’ hợp với đáy một góc
60
0
. Gọi
α
là số đo của góc giữa hai đường thẳng
A
C
,
B...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình chữ nhật , AB = a, AD = 2, hình chiếu vuông góc của điểm A trên mặt phẳng ( A ' B ' C ' D ' ) là trung điểm H của A’D’. Biết rằng AA’ hợp với đáy một góc 60 0 . Gọi α là số đo của góc giữa hai đường thẳng A C , B ' D . Khi đó cos α bằng
![]()
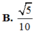
![]()
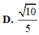
Cho mặt phẳng
α
và đường thẳng
∆
không vuông góc với
α
. Gọi
u
∆
→
,
n
α
→
lần lượt là vectơ chỉ phương của
△
và vectơ pháp tuyến của
α
. Vectơ nào dưới đây là vectơ chỉ phương của
△...
Đọc tiếp
Cho mặt phẳng α và đường thẳng ∆ không vuông góc với α . Gọi u ∆ → , n α → lần lượt là vectơ chỉ phương của △ và vectơ pháp tuyến của α . Vectơ nào dưới đây là vectơ chỉ phương của △ ' là hình chiếu của △ trên α ?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có
S
A
⊥
m
p
(
A
B
C
)
,
S
A
4
α
5
,
A
B
A
C
α
,
B
C
6
α
5
. Gọi M là trung điểm của BC và
α
là góc g...
Đọc tiếp
Cho hình chóp S.ABC có S A ⊥ m p ( A B C ) ,
S A = 4 α 5 ,
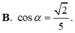
A B = A C = α , B C = 6 α 5 . Gọi M là trung điểm của BC và α là góc giữa hai đường thẳng AC, SM. Tính cos α
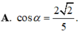
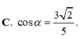
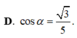
Cho hình trụ trục OO, đường tròn đáy (C) và (C). Xét hình nón đỉnh O, đáy (C) có đường sinh hợp với đáy góc
α
(
0
∘
α
90
∘
)
. Cho biết tỉ số diện tích xung quanh của hình lăng trụ và hình nón bằng
3
. Tính giá trị
α
. A.
30
∘
. A. ...
Đọc tiếp
Cho hình trụ trục OO', đường tròn đáy (C) và (C'). Xét hình nón đỉnh O', đáy (C) có đường sinh hợp với đáy góc α ( 0 ∘ < α 90 ∘ ) . Cho biết tỉ số diện tích xung quanh của hình lăng trụ và hình nón bằng 3 . Tính giá trị α .
A. 30 ∘ .
A. 45 ∘ .
C. 60 ∘ .
A. Kết quả khác



