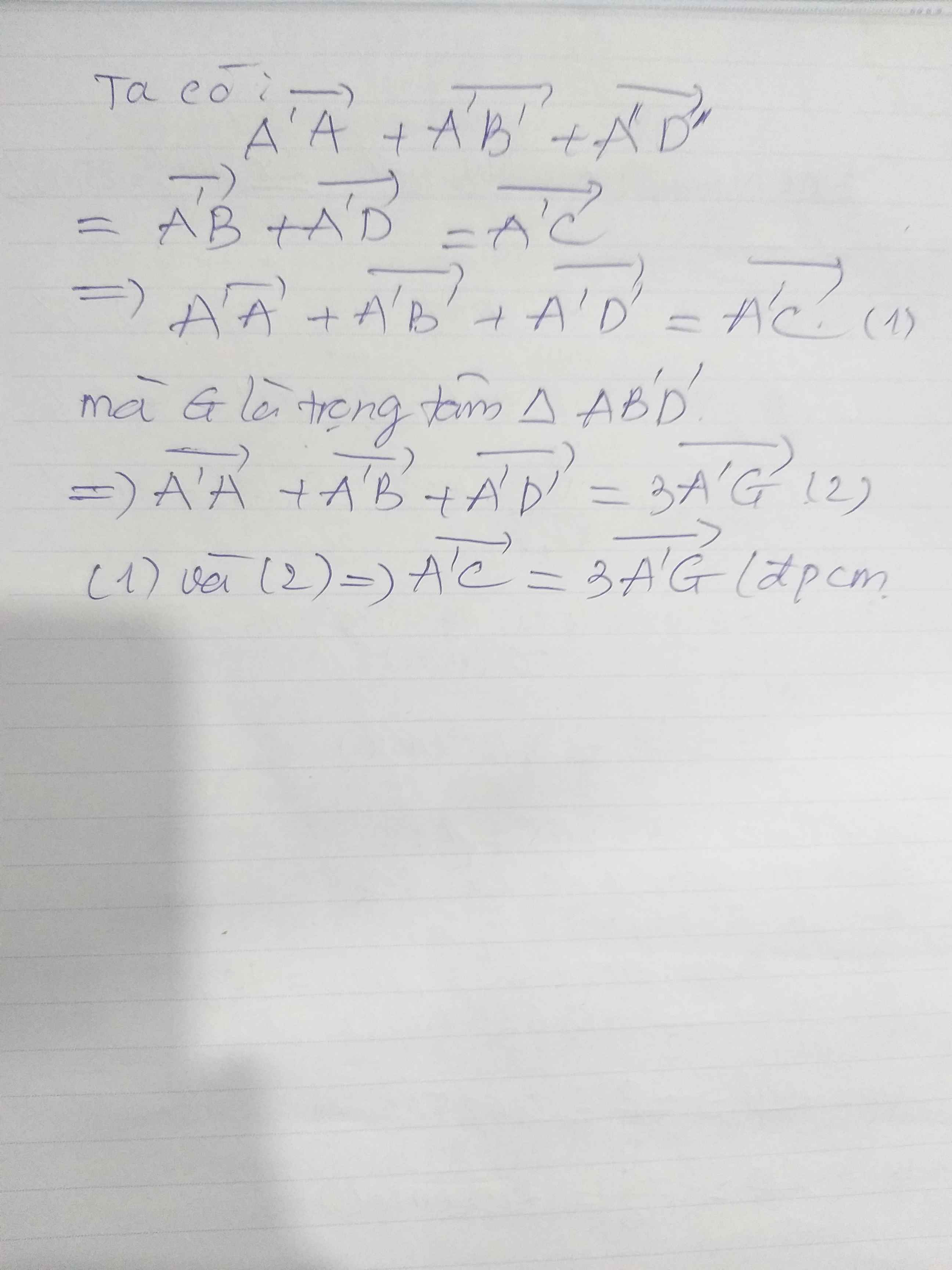Các câu hỏi tương tự
cho lăng trụ ABCD.A'B'C'D', đáy ABCD là hình thoi , có AB=AC=a và A'A=A'B=A'C=a , G là trọng tâm tam giác ABC . tính gióc giữa 2 mặt phẳng (AA'G) và (A'CD)
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Chứng minh hai mặt phẳng (AB'D') và (BC'D) song song.
Cho hình lập phương ABCD.ABCD có cạnh bên bằng a (tham khảo hình vẽ bên). Gọi
α
là góc giữa đường thẳng AC và mặt phẳng (ABCD) thì:
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bên bằng a (tham khảo hình vẽ bên). Gọi α là góc giữa đường thẳng A'C và mặt phẳng (A'B'C'D') thì:
![]()

![]()
![]()
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
. Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD. Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 . Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D'. Khi đó
![]()
![]()
![]()
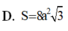
Cho hình lập phương ABCD.ABCD với O là tâm hình vuông ABCD. Biết rằng tứ diện OBCD có thể tích bằng 6
a
3
. Tính thể tích V của khối lập phương ABCD.ABCD. A. V 12
a
3
B. V 6
3
a
3
C. V 2
3
a
3
D. V 9
3...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCD có thể tích bằng 6 a 3 . Tính thể tích V của khối lập phương ABCD.A'B'C'D'.
A. V = 12 a 3
B. V = 6 3 a 3
C. V = 2 3 a 3
D. V = 9 3 a 3
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy là hình vuông cạnh
a
3
. Hình chiếu vuông góc của điểm A lên mặt phẳng
(
A
B
C
D
)
trùng với tâm O của hình vuông
A
B
C
D
. Biết rằng...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a 3 . Hình chiếu vuông góc của điểm A lên mặt phẳng ( A ' B ' C ' D ' ) trùng với tâm O của hình vuông A ' B ' C ' D ' . Biết rằng khoảng cách từ trọng tâm G của tam giác AB’D’ đến mặt phẳng (AA’D) bằng a 2 . Khoảng cách từ điểm O đến mặt phẳng ( A D C ' B ' ) bằng

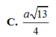
![]()
Cho hình lập phương ABCD.ABCD có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (ABD) và (BCD) bằng:
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có tất cả các cạnh bằng 2. Khoảng cách giữa hai mặt phẳng (AB'D') và (BC'D') bằng:
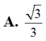
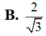

![]()
Cho hình lập phương
ABCD
.
A
B
C
D
.
Gọi I, J lần lượt là trung điểm của các cạnh AD, BC. Phép tịnh tiến theo vectơ
u
→
1
2
A
D
→
biến tam giác AIJ thành tam giác A. C’CD B. CD’P với P là trung điểm của B’C’ C. KDC với K là trung điểm của A’D’ D. DC’D’
Đọc tiếp
Cho hình lập phương ABCD . A ' B ' C ' D ' . Gọi I, J lần lượt là trung điểm của các cạnh AD, BC. Phép tịnh tiến theo vectơ u → = 1 2 A D → biến tam giác A'IJ thành tam giác
A. C’CD
B. CD’P với P là trung điểm của B’C’
C. KDC với K là trung điểm của A’D’
D. DC’D’
Cho hình lập phương ABCD.ABCD có độ dài mỗi cạnh là 10cm. Gọi O là tâm mặt cầu đi qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu là: A.
S
150
π
cm
2
B.
S
100
3
π
cm
2
C.
S
300
π
cm...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có độ dài mỗi cạnh là 10cm. Gọi O là tâm mặt cầu đi qua 8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu là:
A. S = 150 π cm 2
B. S = 100 3 π cm 2
C. S = 300 π cm 2
D. S = 250 π cm 2
Cho hình lập phương ABCD.ABCD, gọi M và N lần lượt là tâm của các hình vuông ABCD và ABCD. Mặt phẳng (AMN) chia khối lập phương thành hai phần có thể tích là
V
1
và
V
2
. Tính tỷ số
V
2
V
1
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và A'B'C'D'. Mặt phẳng (A'MN) chia khối lập phương thành hai phần có thể tích là V 1 và V 2 . Tính tỷ số V 2 V 1 .
![]()
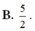
![]()
![]()