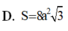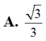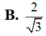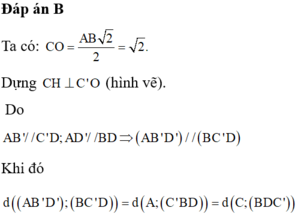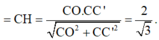Các câu hỏi tương tự
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Chứng minh hai mặt phẳng (AB'D') và (BC'D) song song.
giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách giữa hai mặt phẳng nói trên.
Cho hình lập phương ABCD.ABCD có cạnh bằng
3
. Mặt phẳng
α
cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng
α
biết
α
tạo với mặt (ABBA) một góc
60
0
.
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 3 . Mặt phẳng α cắt tất cả các cạnh bên của hình lập phương. Tính diện tích thiết diện của hình lập phương cắt bởi mặt phẳng α biết α tạo với mặt (ABB'A') một góc 60 0 .
![]()
Giải bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Tính khoảng cách từ đỉnh A đến các mặt phẳng (A'BD) và (B'D'C).
Cho hình lập phương ABCD.ABCD có cạnh bằng a (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng BD và AC bằng: A. a B.
a
2
C.
a
3
2
D.
a
3
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a (tham khảo hình vẽ). Khoảng cách giữa hai đường thẳng BD và A'C' bằng:
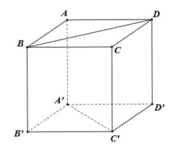
A. a
B. a 2
C. a 3 2
D. a 3
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là A.
90
0
B.
60
0
C.
30
0
D.
45
0
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là
A. 90 0
B. 60 0
C. 30 0
D. 45 0
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và
A
C
bằng A....
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A ' C ' bằng
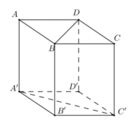
A. 3 a
B. a
C. 3 2 a
D. 2 a
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BD và BC
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BD' và B'C
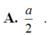
![]()
![]()
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
. Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD. Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 . Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D'. Khi đó
![]()
![]()
![]()