Các câu hỏi tương tự
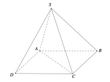
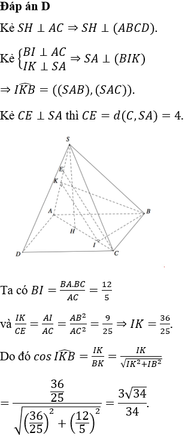
Cho hình chóp S.ABCD có đáy là hình chữ nhật,AB3,BC4. Tam giác SAC nằm trong mặt phẳng vuông góc với đáy, khoảng cách từ điểm C đến đường thẳng SA bằng 4. Côsin góc giữa hai mặt phẳng (SAB) và (SAC) bằng A.
3
17
17
B.
3
34
34
C.
2
34
17...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật,AB=3,BC=4. Tam giác SAC nằm trong mặt phẳng vuông góc với đáy, khoảng cách từ điểm C đến đường thẳng SA bằng 4. Côsin góc giữa hai mặt phẳng (SAB) và (SAC) bằng
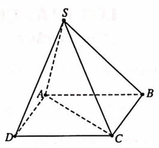
A. 3 17 17
B. 3 34 34
C. 2 34 17
D. 5 34 17
Cho hình chóp S.ABC có AB2a,BCa,
A
B
C
^
120
0
. Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC),d(C,SA)2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng A.
777
37
B.
4
37
37
C.
21...
Đọc tiếp
Cho hình chóp S.ABC có AB=2a,BC=a, A B C ^ = 120 0 . Biết mặt phẳng (SAC) vuông góc với mặt phẳng (ABC),d(C,SA)=2. Côsin góc giữa hai mặt phẳng (SAC) và (SAB) bằng
A. 777 37
B. 4 37 37
C. 21 10
D. 10 11
Cho hình chóp S.ABCD có đáy hình chữ nhật, AB a; AD 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC) A.
d
a
1315
89
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy hình chữ nhật, AB = a; AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = 2 a 1315 89
C. d = 2 a 1513 89
D. d = a 1513 89
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật
A
B
a
,
A
D
a
2
. Góc giữa hai mặt phẳng (SAC) và (ABCD) bằng
60
0
. Gọi H là trung điểm của AB. Biết rằng tam giác SAB cân tại H và nằm trong mặt phẳng vuông góc với đáy. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp A.HAC A.
9
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật A B = a , A D = a 2 . Góc giữa hai mặt phẳng (SAC) và (ABCD) bằng 60 0 . Gọi H là trung điểm của AB. Biết rằng tam giác SAB cân tại H và nằm trong mặt phẳng vuông góc với đáy. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp A.HAC
A. 9 2 a 8
B. 62 a 16
C. 62 a 8
D. 31 a 32
Cho hình chóp S.ABCD có đáy là hình chữ nhật,
A
B
a
,
A
D
2
a
.
Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
45
°
.Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC). A.
d
a
1315...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a , A D = 2 a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 ° .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC).
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
Cho hình chóp S.ABC có thể tích bằng 3 và AB3,AC4,BC5. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là một điểm nằm trong tam giác ABC. Góc giữa các mặt phẳng (SAB),(SAC) và đáy lần lượt bằng
30
°
,
60
°
. Tính cotang góc giữa hai mặt phẳng (SBC) và (ABC). A.
24
-
13
3
15
B.
8...
Đọc tiếp
Cho hình chóp S.ABC có thể tích bằng 3 và AB=3,AC=4,BC=5. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là một điểm nằm trong tam giác ABC. Góc giữa các mặt phẳng (SAB),(SAC) và đáy lần lượt bằng 30 ° , 60 ° . Tính cotang góc giữa hai mặt phẳng (SBC) và (ABC).
A. 24 - 13 3 15
B. 8 - 5 3 5
C. 24 + 13 3 15
D. 8 + 5 3 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
A
B
1
,
B
C
3
mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
α
là số đo của góc giữa hai mặt phẳng (SAB) và (SBC). Khi đó
cos
α
bằng A.
65
65
B.
65
10...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 1 , B C = 3 mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là số đo của góc giữa hai mặt phẳng (SAB) và (SBC). Khi đó cos α bằng
A. 65 65
B. 65 10
C. 65 20
D. 2 65 65
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB1,
B
C
3
mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng A.
2
15
5
B.
3
C.
2
15
3
D. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=1, B C = 3 mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng
A. 2 15 5
B. 3
C. 2 15 3
D. 3 2
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
A
B
3
c
m
,
B
C
4
c
m
,
S
C
5
c
m
. Tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với (ABCD). Các mặt (SAB) và (SAC)tạo với nhau một góc
α
sao cho
α
3
29
. Tính thể tích khối chóp SA...
Đọc tiếp
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = 3 c m , B C = 4 c m , S C = 5 c m . Tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với (ABCD). Các mặt (SAB) và (SAC)tạo với nhau một góc α sao cho α = 3 29 . Tính thể tích khối chóp SABCD.
A.16 c m 2 .
B. 15 29 c m 2 .
C.20 c m 2 .
D. 18 5 c m 2 .