Question

Cho hình chóp  S . A B C D có đáy là hình thang vuông tại A và B. Biết A D = 2 a , A B = B C = S A = a . Cạnh bên SA vuông góc với mặt phẳng đáy, gọi M là trung điểm cạnh AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).

A. h = a 3 .

B. h = a 6 3 .

C. h = a 6 6 .

D.  h = a 3 6

Answer 1

Đáp án C

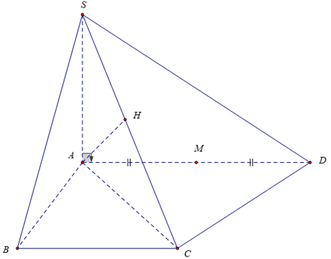
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .

C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D

Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .

Tam giác SAC vuông tại

 A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3

Mặt khác: A D ∩ S C D = D  và M là trung điểm AD nên:

d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6