Cho H(2+t;1+2t;t) ∈ ∆ . Ta có: A H → =(1+t;1+2t;t) đường thẳng ∆ có vecto chỉ phương a → =(1;2;1). Vì H là hình chiếu vuông góc của A trên ∆ nên AH vuông góc với ∆ <=> A H → . a → = 0
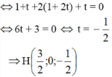
Cho H(2+t;1+2t;t) ∈ ∆ . Ta có: A H → =(1+t;1+2t;t) đường thẳng ∆ có vecto chỉ phương a → =(1;2;1). Vì H là hình chiếu vuông góc của A trên ∆ nên AH vuông góc với ∆ <=> A H → . a → = 0
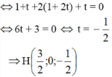
Cho điểm M(2; -1; 1) và đường thẳng
∆ : x - 1 2 = y + 1 - 1 = z 2
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng ∆
Trong không gian với hệ tọa độ Oxyz,
cho điểm A(3;-2;5) và đường thẳng (d): x = - 8 + 4 t y = 5 - 2 t z = t .
Tọa độ hình chiếu vuông góc của điểm A
lên đường thẳng (d).
![]()
![]()
![]()
![]()
Cho điểm A(1;0;0) và đường thẳng ∆ : x = 2 + t y = 1 + 2 t z = t Tìm tọa độ điểm A' đối xứng với A qua đường thẳng ∆
Trong không gian vỏi hệ tọa độ Oxỵz, cho đường thẳng ∆ : x + 1 2 = y + 2 - 1 = z 2 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A(2;-3;1) lên ∆ .
A. H(-3;-1;-2)
B. H(-1;-2;0)
C. H(3;-4;4)
D. H(1;-3;2)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 1 2 = y - 1 = z + 2 3 và điểm A(1;0;0).
Mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng d có phương trình là
A. z - 2z - 1 = 0
B. x + y - z - 1 = 0
C. 2x - y + 3z - 2 = 0
D. 2x + y + 3z - 2 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;0;4) và đường thẳng d có phương trình là x 1 = y - 1 - 1 = z + 1 2 . Tìm hình chiếu vuông góc H của M lên đường thẳng d.
A. H(1;0;1)
B. H(-2;3;0)
C. H(0;1;-1)
D. H(2;-1;3)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x = 1 + t y = 2 z = 3 - t và điểm A(-1;2;-1). Tìm tọa độ điểm I là hình chiếu của I lên ∆
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 2 = y + 2 1 = z + 1 - 1 và mặt phẳng (P):x+y+z+2=0. Đường thẳng ∆ nằm trong mặt phẳng (P) vuông góc với đường thẳng d đồng thời khoảng cách từ giao điểm I của d với (P) đến ∆ bằng 42 . Gọi M(5;b;c) là hình chiếu vuông góc của I trên ∆ . Giá trị của bc bằng
A. -10
B. 10
C. 12
D. -20
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4;6;2) và B(2;-2;0) và mặt phẳng (P):x+y+z=0. Xét đường thẳng d thay đổi thuộc (P) và đi qua B, gọi H là hình chiếu vuông góc của A trên d. Biết rằng khi d thay đổi thì H thuộc một đường tròn cố định. Tính bán kính R của đường tròn đó.
A. R= 6
B. R=2
C. R=1
D. R= 3