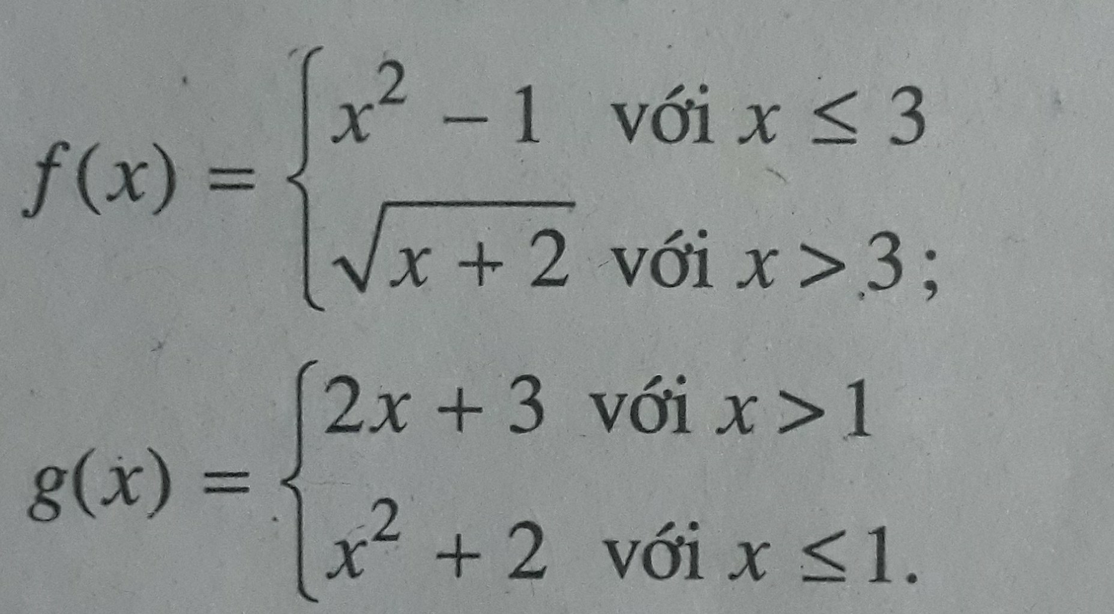Đáp án: A (vì f(0) = -1; f(7) = 3 và g(1) = 3).
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hàm số f(x) ={\(\dfrac{-2\left(x-3\right)}{\sqrt{x^2-1}}\)\(\dfrac{-1\le x< 1}{x\ge1}\)giá trị của f(-1), f(1) lần lượt là
A. 0 và 8 B. 8 và 0 C. 0 và 0 D. 8 và 4
cho hàm số \(\begin{matrix}\\\end{matrix}\)f(x) \(\left\{{}\begin{matrix}\sqrt{x+1}-2.khi,x\ge-1\\3x^2-x+1.khi,x< -1\end{matrix}\right.\)
giá trị f(-3) + f(0) bằng
Cho phương trình của (P): y a
x
2
+ bx + c (a
≠
0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng
a
2
+
b
2
+
c
2
A.
a
2
+
b
2
+
c...
Đọc tiếp
Cho phương trình của (P): y = a x 2 + bx + c (a ≠ 0) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A (2; 0), B (−2; −8). Tình tổng a 2 + b 2 + c 2
A. a 2 + b 2 + c 2 = 3
B. a 2 + b 2 + c 2 = 29 16
C. a 2 + b 2 + c 2 = 48 29
D. a 2 + b 2 + c 2 = 5 a 2 + b 2 + c 2 = 209 16
Xác định Parabol (P) : y = ax^2 + bx + c ( a khác 0 ) biết (P) đi qua :
a, điểm E (0; 6) và hàm số y = ax^2 - bx + c đạt giá trị nhỏ nhất là 4 khi x = -2
b, điểm F (1; 16) và cắt Ox tại các điểm có hoành độ là -1 và 5.
Cho hàm số:
f
(
x
)
x
x
+
1
,
x
≥
0
1
x
−...
Đọc tiếp
Cho hàm số: f ( x ) = x x + 1 , x ≥ 0 1 x − 1 , x < 0 . Giá trị f ( 0 ) , f ( 2 ) , f ( − 2 ) là:
A. f ( 0 ) = 0 , f ( 2 ) = 2 3 , f ( − 2 ) = 2
B. f ( 0 ) = 0 , f ( 2 ) = 2 3 , f ( − 2 ) = − 1 3
C. f ( 0 ) = 0 , f ( 2 ) = 1 , f ( − 2 ) = − 1 3
D. f ( 0 ) = 0 , f ( 2 ) = 1 , f ( − 2 ) = 2
Cho hàm số y
x
2
− 2(m +
1
m
)x + m (m 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là
y
1
,
y
2
thỏa mãn
y
1
-
y
2
8. Khi đó giá trị của m bằng A. m 1 B. m
∈...
Đọc tiếp
Cho hàm số y = x 2 − 2(m + 1 m )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là y 1 , y 2 thỏa mãn y 1 - y 2 = 8. Khi đó giá trị của m bằng
A. m = 1
B. m ∈ ∅
C. m = 2
D. m = 1, m = 2
Biết rằng hàm số y = a x 2 + bx + c (a ≠ 0) đạt giá trị lớn nhất bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; −1). Tính tổng S = a + b + c.
A. S = -1
B. S = 4
C. S = - 4
D. S = 2
Cho hàm số Y=x^2-2(m+1/m)x +m (m>0) xác định trên [-1;1]. Giá trị lớn nhất. giá trị nhỏ nhất của hàm số trên [-1;1] lần lượt là y1'y2 thỏa mãn y1+y2=8. khi đó giá trị của m bằng
Cho hàm số \(f\left(x\right)\) là hàm số bậc hai với hệ số \(a>0\), thỏa mãn \(\left|f\left(x\right)\right|\le1,\forall x\in\left[-1;1\right]\) và biểu thức \(P=\dfrac{8}{3}a^2+2b^2\) đạt giá trị lớn nhất. Tính giá trị của biểu thức \(Q=5a+11b+c.\)