Đáp án C
Nếu ba đường thẳng a,b,c đôi một cắt nhau và không đồng phẳng thì chúng chỉ có thể đồng quy tại một điểm.

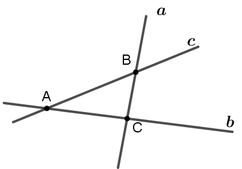
Đáp án C
Nếu ba đường thẳng a,b,c đôi một cắt nhau và không đồng phẳng thì chúng chỉ có thể đồng quy tại một điểm.


Cho hàm số y = x 3 - 3 x + 2 C . Biết rằng đường thẳng d : y = m x + 1 cắt C tại ba điểm phân biệt A, B, C. Tiếp tuyến tại ba điểm A, B, C của đồ thị cắt đồ thị C lần lượt tại các điểm A', B', C'(tương ứng khác A, B, C). Biết rằng A', B', C' thẳng hàng, tìm giá trị của tham số m để đường thẳng đi qua ba điểm A', B', C' vuông góc với đường thẳng ∆ : x + 2018 y - 2019 = 0
A. m = 1009 2
B. m = 1009 4
C. m = 2009 4
D. m = 2019 4
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng d : x = - t y = 2 + t z = 3 - t Tọa độ giao điểm của mặt phẳng (ABC) và đường thẳng d là
A. (3;-1;6)
B. (-1;3;6)
C. (3;-1;3)
D. (-3;-1;6)
Trong không gian, cho các mệnh đề sau:
I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).
IV. Qua điểm A không thuộc mặt phẳng ( α ) , kẻ được đúng một đường thẳng song song với .
Số mệnh đề đúng là
A. 2
B. 0
C. 1
D. 3
Cho d là đường thẳng đi qua điểm A - 1 ; 3 và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị C của hàm số y = x 3 - 3 x + 1 tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính tổng bình phương các phần tử thuộc tập hợp S.
A. 16 9
B. 34 9
C. 38 9
D. 34 3
Cho hàm số y = x + 1 x - 1 và đường thẳng y = -2x + m Tìm giá trị của m để đồ thị hàm số đã cho cắt nhau tại 2 điểm A, B phân biệt; đồng thời, trung điểm của đoạn thẳng AB có hoành độ bằng 5 2
A. m = -9
B. m = 9
C. m = 8
D. m = 10
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), A’(0;0;b). Gọi (P) là mặt phẳng chứa d và d’; H là giao điểm của đường thẳng AA’ và mặt phẳng (P). Một đường thẳng thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d’ lần lượt tại B, B’. Hai đường thẳng AB, A’B’ cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính a+b
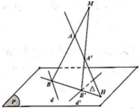
A. 8
B. 9
C. -9
D. 6
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
x
=
-
3
+
2
t
y
=
-
1
+
t
z
=
3
+
t
và mặt phẳng có phương trình (a): x + 2y - z + 5 = 0 . Gọi A là giao điểm của ![]() và (a). Tìm điểm
B
∈
∆
;
C
∈
a
sao cho
B
A
=
2
B
C
=
6
và
A
B
C
^
=
60
o
.
và (a). Tìm điểm
B
∈
∆
;
C
∈
a
sao cho
B
A
=
2
B
C
=
6
và
A
B
C
^
=
60
o
.
A. B ( -3;-1;3 ); C - 5 2 ; 0 ; 5 2 hoặc B ( -1;0;4 ); C 1 2 ; 0 ; 11 2
B. B ( -3;-1;3 ); C - 5 2 ; 0 ; 5 2 hoặc B ( 1;1;5 ); C 1 2 ; 0 ; 11 2
C. B ( -3;-1;3 ); C - 5 2 ; 0 ; 5 2 hoặc B ( -7;-3;1 ); C 1 2 ; 0 ; 11 2
D. B ( -3;-1;3 ); C - 5 2 ; 0 ; 5 2 hoặc B ( 3;2;6 ); C 1 2 ; 0 ; 11 2
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x − 2 1 = y − 5 2 = z − 2 1 , d ' : x − 2 1 = y − 1 − 2 = z − 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d¢; H là giao điểm của đường thẳng AA¢ và mặt phẳng (P). Một đường thẳng D thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d¢ lần lượt tại B, B¢. Hai đường thẳng A B , A ' B ' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có véc tơ chỉ phương u → 15 ; − 10 ; − 1 (tham khảo hình vẽ). Tính T = a + b

A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng ∆ thay đổi trên (P) nhưng luôn đi qua H đồng thời ∆ cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính T= a+b
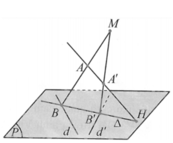
A. T = 8
B. T = 9
C. T = - 9
D. T = 6