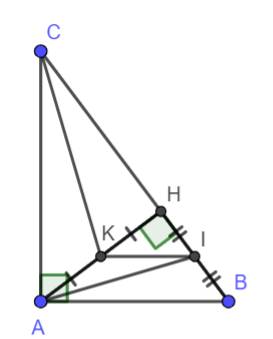
a) \(\Delta ABC\) vuông tại A (gt)
\(\Rightarrow BC^2=AB^2+AC^2\left(Pythagore\right)\)
\(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=81\)
\(\Rightarrow AB=9\left(cm\right)\)
b) Sửa đề: \(AB^2=BH.BC\)
Xét hai tam giác vuông: \(\Delta ABC\) và \(\Delta HBA\) có:
\(\widehat{B}\) chung
\(\Rightarrow\Delta ABC\) ∽ \(\Delta HBA\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{AB}\)
\(\Rightarrow AB^2=BH.BC\)
c) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CHA\) có:
\(\widehat{HAB}=\widehat{HCA}\) (cùng phụ \(\widehat{ABC}\))
\(\Rightarrow\Delta AHB\) ∽ \(\Delta CHA\left(g-g\right)\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\)
\(\Rightarrow AH^2=HB.HC\)
d) Do \(AB^2=BH.BC\left(cmt\right)\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=5,4\left(cm\right)\)
\(\Rightarrow CH=BC-BH=15-5,4=9,6\left(cm\right)\)
Do \(AH^2=BH.CH\left(cmt\right)\)
\(=5,4.9,6=51,84\)
\(\Rightarrow AH=7,2\left(cm\right)\)
Do \(I\) là trung điểm của BH (gt)
\(\Rightarrow BI=\dfrac{BH}{2}=\dfrac{5,4}{2}=2,7\left(cm\right)\)
Do \(K\) là trung điểm của AH (gt)
\(\Rightarrow AK=\dfrac{AH}{2}=\dfrac{7,2}{2}=3,6\left(cm\right)\)
Ta có:
\(\dfrac{IB}{AK}=\dfrac{2,7}{3,6}=\dfrac{3}{4}\)
\(\dfrac{AB}{AC}=\dfrac{9}{12}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{IB}{AK}=\dfrac{AB}{AC}\) \(=\dfrac{3}{4}\)
Xét \(\Delta AIB\) và \(\Delta CKA\) có:
\(\dfrac{IB}{AK}=\dfrac{AB}{AC}=\dfrac{3}{4}\left(cmt\right)\)
\(\widehat{IBA}=\widehat{KAC}\) (cùng phụ \(\widehat{ACB}\))
\(\Rightarrow\Delta AIB\) ∽\(\Delta CKA\left(c-g-c\right)\)













