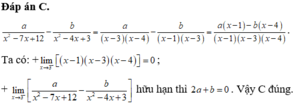Các câu hỏi tương tự
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn
lim
x
→
3
−
a
x
2
−
7
x
+
12
−
b
x...
Đọc tiếp
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để giới hạn lim x → 3 − a x 2 − 7 x + 12 − b x 2 − 4 x + 3 là hữu hạn.
A. 4 a + b = 0
B. 3 a + b = 0
C. 2 a + b = 0
D. a + b = 0
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để
lim
x
→
2
a
x
2
-
6
x
+
8
-
b...
Đọc tiếp
Cho a và b là các số thực khác 0. Tìm hệ thức liên hệ giữa a và b để lim x → 2 a x 2 - 6 x + 8 - b x 2 - 5 x + 6 là hữu hạn
A. a-2b = 0
B. a+b = 0
C. a-3b = 0
D. a-b = 0
Cho hàm số yf(x) liên tục trên đoạn
a
;
b
và f(x)0
∀
x
∈
a
;
b
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số yf(x), trục hoành và 2 đường thẳng xa, xb (ab). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x
Cho hàm số
y
f
(
x
)
liên tục trên đoạn [a;b] có đồ thị như hình bên và
c
∈
a
;
b
. Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số
y
f
(
x
)
và các đường thẳng
y
0
,
x
a...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên đoạn [a;b] có đồ thị như hình bên và c ∈ a ; b . Gọi S là diện tích của hình phẳng (H) giới hạn bởi đồ thị hàm số y = f ( x ) và các đường thẳng y = 0 , x = a , x = b . . Mệnh đề nào sau đây sai?
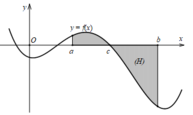
A. S = ∫ a c f x d x + ∫ c b f x d x
B. S = ∫ a c f x d x − ∫ c b f x d x
C. S = ∫ a b f x d x
D. S = ∫ a c f x d x + ∫ b c f x d x
Cho a, b, c là các số thực khác 0. Để giới hạn
lim
x
→
−
∞
x
2
−
3
x
+
a
x
b
x
−
1
3...
Đọc tiếp
Cho a, b, c là các số thực khác 0. Để giới hạn lim x → − ∞ x 2 − 3 x + a x b x − 1 = 3 thì
A. a − 1 b = 3.
B. a + 1 b = 3.
C. − a − 1 b = 3.
D. a − 1 − b = 3.
Cho hàm số
C
:
y
f
x
liên tục trên đoạn [a;b]. Xét hình phẳng (H) giới hạn bởi các đường
C
;
y
0
;
x
a
;
x
b
. Quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích là: A.
∫
a
b...
Đọc tiếp
Cho hàm số C : y = f x liên tục trên đoạn [a;b]. Xét hình phẳng (H) giới hạn bởi các đường C ; y = 0 ; x = a ; x = b . Quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích là:
A. ∫ a b f 2 x d x
B. ∫ a b f x d x
C. π ∫ a b f 2 x d x
D. π ∫ a b f x d x
Cho hai hàm số y f(x) và y g(x) liên tục trên đoạn [a;b]. Diện tích của hình phẳng giới hạn bởi đồ thị các hàm số y f(x) và y g(x) và hai đường thẳng x a, x b (a b) được tính theo công thức là A.
S
∫
a
b
f
(
x
)
-
g
(
x...
Đọc tiếp
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a;b]. Diện tích của hình phẳng giới hạn bởi đồ thị các hàm số y = f(x) và y = g(x) và hai đường thẳng x = a, x = b (a < b) được tính theo công thức là
A. S = ∫ a b f ( x ) - g ( x ) d x
B. S = π ∫ a b f ( x ) - g ( x ) d x
C. S = ∫ a b | f ( x ) - g ( x ) | d x
D. S = ∫ a b f ( x ) - g ( x ) d x
Trong không gian với hệ toạ độ Oxyz, xét ba điểm A(a;0;0),B(0;b;0),C(0;0;c) với a,b,c là các số thực thay đổi thoả mãn
1
a
-
2
b
+
2
c
1
. Biết rằng mặt cầu (S):
(
x
-
2
)
2
+
y
2
+
(
z
-
4...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, xét ba điểm A(a;0;0),B(0;b;0),C(0;0;c) với a,b,c là các số thực thay đổi thoả mãn 1 a - 2 b + 2 c = 1 . Biết rằng mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z - 4 ) 2 = 25 cắt mặt phẳng (ABC) theo giao tuyến là một đường tròn có bán kính bằng 4. Giá trị của biểu thức a+b+c bằng
A. 5.
B. 1.
C. 2.
D. 4.
Cho hình phẳng D giới hạn bởi các đường
y
2
x
2
+
x
sin
x
-
x
-
1
cos
x
x...
Đọc tiếp
Cho hình phẳng D giới hạn bởi các đường y = 2 x 2 + x sin x - x - 1 cos x x sin x + cos x , trục hoành và hai đường thẳng x = 0 và x = π 4 . Biết rằng diện tích của hình phẳng D bằng π 2 + 4 π 16 + a ln 2 + b ln π + 4 , với a, b là các số hữu tỷ. Mệnh đề nào dưới đây đúng?
A. 2 a + b = 12
B. 2 a - b = - 6
C. 2 a - b = - 12
D. 2 a + b = 6