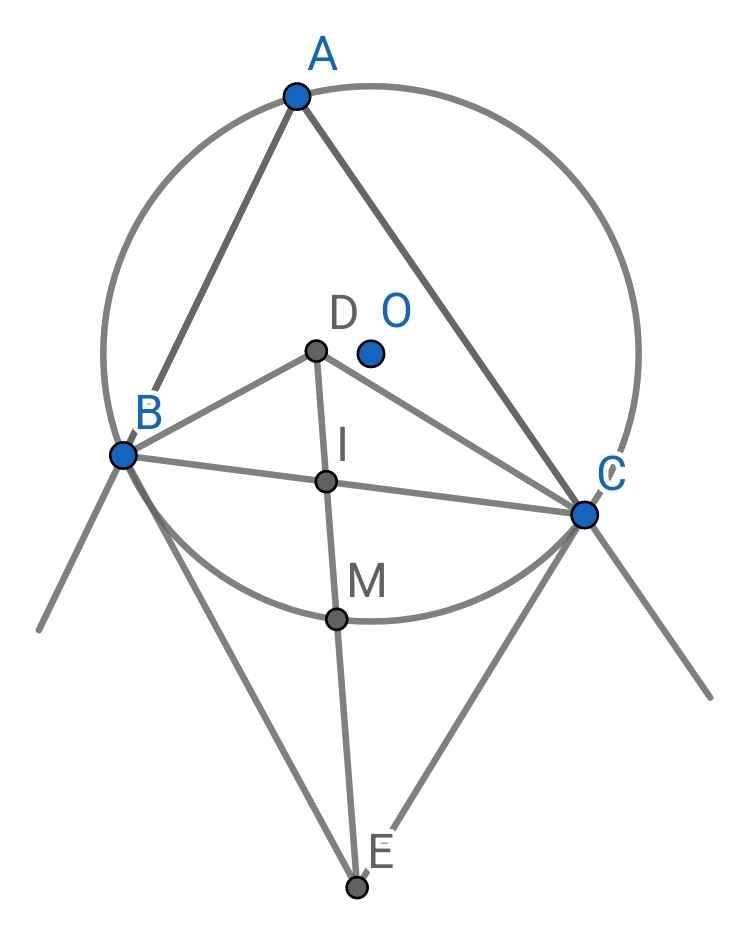
Câu hỏi: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi E, D lần lượt là giao điểm của các tia phân giác trong và ngoài của hai góc B và C. Đường thẳng ED cắt BC tại I, cắt cung nhỏ BC ở M.
a) Vẽ hình (vẽ giúp em vs em vẽ mãi mà ko ra ;-;)
b) Chứng minh tứ giác BECD nội tiếp được trong đường tròn.
c) Chứng minh BI . IC = ID . IE
a: Gợi ý cách vẽ: Bạn vẽ hai tia phân giác trong của hai góc B và góc C cắt nhau tại E trước, rồi lần lượt vẽ hai đường vuông góc tại chính điểm đó luôn, rồi lấy giao là D là xong
b: 
a)
b) Do BD là tia phân giác của ∠ABC (gt)
BE là tia phân giác của góc ngoài tại B của ∆ABC (gt)
⇒ ∠DBE= 90⁰
Do CD là tia phân giác của ∠ACB (gt)
CE là tia phân giác của góc ngoài tại đỉnh C của ∆ABC (gt)
⇒ ∠DCE = 90⁰
Tứ giác BECD có:
∠DBE + ∠DCE = 90⁰ + 90⁰ = 180⁰
BECD nội tiếp
c) Xét ∆BIE và ∆DIC có:
∠BIE = ∠DIC (đối đỉnh)
∠IBE = ∠IDC (hai góc nội tiếp cùng chắn cung CE của đường tròn ngoại tiếp tứ giác BECD)
⇒ ∆BIE ∽ ∆DIC (g-g)
⇒ BI/ID = IE/IC
⇒ BI.IC = ID.IE















