o: \(\dfrac{-35}{120}=\dfrac{-35\cdot3}{120\cdot3}=\dfrac{-105}{360}\)
\(\dfrac{19}{-45}=\dfrac{-19}{45}=\dfrac{-19\cdot8}{45\cdot8}=\dfrac{-152}{360}\)
mà -105>-152
nên \(-\dfrac{35}{120}>-\dfrac{19}{45}\)
p: \(\dfrac{-12}{48}=\dfrac{-1}{4}=\dfrac{-13}{52}\)
\(\dfrac{-7}{26}=\dfrac{-7\cdot2}{26\cdot2}=\dfrac{-14}{52}\)
mà -13>-14
nên \(-\dfrac{12}{48}>-\dfrac{7}{26}\)
q: \(\dfrac{-8}{-90}=\dfrac{8}{90}\)
\(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{30}{90}\)
mà 8<30
nên \(\dfrac{-8}{-90}< \dfrac{14}{42}\)
r: \(\dfrac{-34}{68}=\dfrac{-1}{2}=\dfrac{-28}{56}\)
\(\dfrac{28}{-51}=\dfrac{-28}{51}\)
56>51
=>\(\dfrac{28}{56}< \dfrac{28}{51}\)
=>\(-\dfrac{28}{56}>-\dfrac{28}{51}\)
=>\(\dfrac{-34}{68}>\dfrac{28}{-51}\)
t: \(\dfrac{-19}{60}< 0\)
\(0< \dfrac{42}{45}=\dfrac{-42}{-45}\)
Do đó: \(\dfrac{-19}{60}< \dfrac{-42}{-45}\)
v: \(\dfrac{1}{-2024}< 0\)
\(0< \dfrac{-2023}{-45}=\dfrac{2023}{45}\)
Do đó: \(\dfrac{1}{-2024}< \dfrac{-2023}{-45}\)
x: Đặt \(A=\dfrac{2024^{2025}+1}{2024^{2026}+1};B=\dfrac{2024^{2000}+1}{2024^{2001}+1}\)
\(2024A=\dfrac{2024^{2026}+2024}{2024^{2026}+1}=1+\dfrac{2023}{2024^{2026}+1}\)
\(2024B=\dfrac{2024^{2001}+2024}{2024^{2001}+1}=1+\dfrac{2023}{2024^{2001}+1}\)
\(2024^{2026}+1>2024^{2001}+1\)
=>\(\dfrac{2023}{2024^{2026}+1}< \dfrac{2023}{2024^{2001}+1}\)
=>2024A<2024B
=>A<B
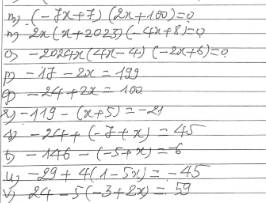
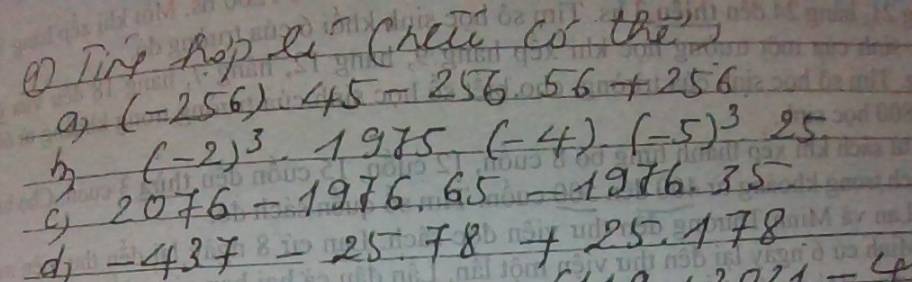cần giúp gấp vs ạ, em cảm ơn nhìu
