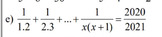\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2020}{2021}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{2020}{2021}\Leftrightarrow\dfrac{x}{x+1}=\dfrac{2020}{2021}\Rightarrow2021x=2020x+2020\Leftrightarrow x=2020\)
\(\Leftrightarrow\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2020}{2021}\)
\(\Leftrightarrow1-\dfrac{1}{x+1}=\dfrac{2020}{2021}\)
\(\Leftrightarrow-\dfrac{1}{x+1}=-\dfrac{1}{2021}\)
\(\Leftrightarrow x+1=2021\)
\(\Leftrightarrow x=2020\)