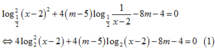Các câu hỏi tương tự
cho phương trình $x^4+(1-2m)x^2+m^2-1$
tìm m để phương trình
a)vô nghiệm
b)có 1 nghiệm
c)có 2 nghiệm
d)có 3 nghiệm
f)có 4 nghiệm
giúp mình giải chi tiết 1 chút nhé và giúp mình luôn trong cách trình bày
Có tất cả bao nhiêu số nguyên m để phương trình
log
(
m
-
x
)
3
log
(
4
-
2
x
-
3
)
có hai nghiệm thực phân biệt. A. 6. B. 2. C. 3. D. 5.
Đọc tiếp
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.
Biết rằng phương trình
2
−
x
+
2
+
x
−
4
−
x
2
m
có nghiệm khi m thuộc [a;b] với
a
,
b
∈
ℝ
. Khi đó giá trị của biểu thức
T
a
+
2...
Đọc tiếp
Biết rằng phương trình 2 − x + 2 + x − 4 − x 2 = m có nghiệm khi m thuộc [a;b] với a , b ∈ ℝ . Khi đó giá trị của biểu thức T = a + 2 2 + b là
A. T = 3 2 + 2
B. T = 6
C. T = 8
D. T = 0
Tìm số nghiệm nguyên của bất phương trình
log
5
2
3
x
-
2
log
2
(
4
-
x
)
-
log...
Đọc tiếp
Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x - 2 log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Cho phương trình:
(
m
−
1
)
log
1
2
2
x
−
2
2
+
4
m
−
5
log
1
2
1
x...
Đọc tiếp
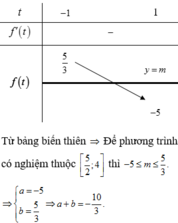
Cho phương trình:
( m − 1 ) log 1 2 2 x − 2 2 + 4 m − 5 log 1 2 1 x − 2 + 4 m − 4 = 0 (với m là tham số). Gọi S = [ a ; b ] là tập các giá trị của m để phương trình có nghiệm trên đoạn 5 2 ; 4 . Tính a+b.
A. 7 3
B. − 2 3
C. − 3
D. 1034 237
Cho phương trình
m
ln
2
x
+
1
-
x
+
2
-
m
ln
x
+
1
-
x
-
2
0
1
. Tập tất cả giá trị của tham số m để phương trình 1 có các n...
Đọc tiếp
Cho phương trình m ln 2 x + 1 - x + 2 - m ln x + 1 - x - 2 = 0 1 . Tập tất cả giá trị của tham số m để phương trình 1 có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn 0 < x 1 < 2 < 4 < x 2 là khoảng a ; + ∞ . Khi đó, a thuộc khoảng
A. (3,8;3,9)
B. (3,7;3,8)
C. (3,6;3,7)
D. (3,5;3,6)
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
Cho phương trình
m
-
1
log
1
2
2
x
-
2
2
+
4
m
-
5
log
1
2
1
x
-
2
+
4
m
-...
Đọc tiếp
Cho phương trình m - 1 log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 + 4 m - 4 = 0 (với m là tham số). Gọi S = a , b là tập hợp các giá trị của m để phương trình có nghiệm trên đoạn 5 2 ; 4 . Tính a + b
A. 7 3
B. - 2 3
C. - 3
D. 1034 237
Cho đường thẩng (d): 2x+y-10 và điểm A(0; -2), B(2; 3).1) Lập phương trình đường thẳng d1 đi qua A và song song với d.2) Lập phương trình đường thẳng d2 đi qua B và vuông góc với d. Từ đó tìm tọa độ hình chiếu H của B trên d.3) Tìm điểm M thuộc trục hoành sao cho khoảng cách từ M đến d bằng 2√5
.4) Tìm điểm N thuộc d sao cho khoảng cách từ N đến A bằng 5.
Đọc tiếp
Cho đường thẩng (d): 2x+y-1=0 và điểm A(0; -2), B(2; 3).
1) Lập phương trình đường thẳng d1 đi qua A và song song với d.
2) Lập phương trình đường thẳng d2 đi qua B và vuông góc với d. Từ đó tìm tọa độ hình chiếu H của B trên d.
3) Tìm điểm M thuộc trục hoành sao cho khoảng cách từ M đến d bằng \(2√5 \).
4) Tìm điểm N thuộc d sao cho khoảng cách từ N đến A bằng 5.