Các câu hỏi tương tự
Cho số phức z thỏa mãn điều kiện 3
≤
|z-3i+1|
≤
5. Tập hợp các điểm biểu diễn của Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
A
.
S
25
π
B
.
S
8
π
D
.
S
4
π...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện 3 ≤ |z-3i+1| ≤ 5. Tập hợp các điểm biểu diễn của Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
A . S = 25 π
B . S = 8 π
D . S = 4 π
D . S = 16 π
Cho số phức z thỏa mãn điều kiện 3
≤
|z-3i+1|
≤
5. Tập hợp các điểm biểu diễn của Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó. A. S 25
π
B. S 8
π
C. S 4
π
D. S 16
π
Đọc tiếp
Cho số phức z thỏa mãn điều kiện 3 ≤ |z-3i+1| ≤ 5. Tập hợp các điểm biểu diễn của
Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
A. S = 25 π
B. S = 8 π
C. S = 4 π
D. S = 16 π
Gọi S là tập hợp các số phức z thỏa mãn
z
-
i
≥
3
và
z
-
2
-
2
i
≤
5
. Kí hiệu
z
1
,
z...
Đọc tiếp
Gọi S là tập hợp các số phức z thỏa mãn z - i ≥ 3 và z - 2 - 2 i ≤ 5 . Kí hiệu z 1 , z 2 là hai số phức thuộc S và là những số phức có môđun lần lượt nhỏ nhất và lớn nhất. Tính giá trị của biểu thức P = z 2 + 2 z 1 .
A. P= 2 6
B. P= 3 2
C. P= 33
D. P=8
Gọi S là tổng các nghiệm phức của phương trình ( z - 1 ) 4 = 5. Tính S.
A. S = 0
B. S = 4
C. S = 2i
D. S = 4 5
Gọi A, B, C là các điểm biểu diễn các số phức là nghiệm cùa phương trình
z
3
8
trên mặt phẳng Oxy. Diện tích S của tam giác ABC bằng bao nhiêu?
Đọc tiếp
Gọi A, B, C là các điểm biểu diễn các số phức là nghiệm cùa phương trình z 3 = 8 trên mặt phẳng Oxy. Diện tích S của tam giác ABC bằng bao nhiêu?
![]()
![]()
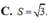
![]()
Cho số phức z=1+i. Gọi S là tập hợp tất cả các điểm biểu diễn số phức w=a+bz+cz2 với a,b,c là các tham số thực thuộc đoạn [0;1]. Tính diện tích hình S?
Gọi S là tổng các số thực m để phương trình
z
2
-
2
z
+
1
-
m
0
có nghiệm phức thỏa mãn
z
2
Tính S.
Đọc tiếp
Gọi S là tổng các số thực m để phương trình z 2 - 2 z + 1 - m = 0 có nghiệm phức thỏa mãn z = 2 Tính S.
![]()
![]()
![]()
![]()
Biết các điểm biểu diễn các nghiệm phức của phương trình z6 1 tạo thành một đa giác lồi có diện tích S. Tính S A. S
3
3
2
B. S
3
4
C. S
π
3
2
D. S
3
Đọc tiếp
Biết các điểm biểu diễn các nghiệm phức của phương trình z6 = 1 tạo thành một đa giác lồi có diện tích S. Tính S
A. S = 3 3 2
B. S = 3 4
C. S = π 3 2
D. S = 3
Trên mặt phẳng tọa độ, các điểm A, B, C theo thứ tự biểu diễn các số phức 2+3i, 3+i, 1+2i.Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z
A. z=1+i
B.z=2+2i
C.z=2-2i
D.z=1-i




