Question

Bài 6. (3,0 điểm) Cho tam giác ABC có ba góc nhọn ( AB <AC ). Đường cao AD,BE,CF, cắt nhau tại H.
a) Chứng minh rằng: BF BA=BD BC;góc BFD=góc BCA .
b) Chứng minh rằng: HB HE =HC HF; gócHEF=góc HCB.
c) Chứng minh rằng: BF.BA+CH.CF=BC^2

Answer 1

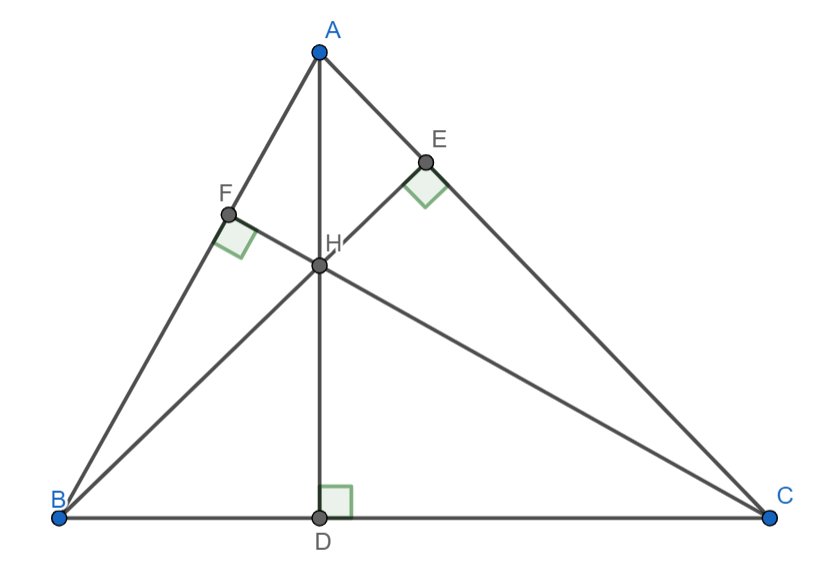
a: Xét ΔBFC vuông tại F và ΔBDA vuông tại D có

\(\widehat{FBC}\) chung

Do đó: ΔBFC~ΔBDA

=>\(\dfrac{BF}{BD}=\dfrac{BC}{BA}\)

=>\(\dfrac{BF}{BC}=\dfrac{BD}{BA}\)

=>\(BF\cdot BA=BD\cdot BC\)

Xét ΔBFD và ΔBCA có

\(\dfrac{BF}{BC}=\dfrac{BD}{BA}\)

\(\widehat{FBD}\) chung

Do đó: ΔBFD~ΔBCA

=>\(\widehat{BFD}=\widehat{BCA}\)

b: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có

\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)

Do đó: ΔHFB~ΔHEC

=>\(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)

=>\(\dfrac{HF}{HB}=\dfrac{HE}{HC}\)

=>\(HF\cdot HC=HE\cdot HB\)

Xét ΔHEF và ΔHCB có

\(\dfrac{HE}{HC}=\dfrac{HF}{HB}\)

\(\widehat{EHF}=\widehat{CHB}\)

Do đó: ΔHEF~ΔHCB

=>\(\widehat{HEF}=\widehat{HCB}\)

c: Xét ΔCDH vuông tại D và ΔCFB vuông tại F có

\(\widehat{DCH}\) chung

Do đó: ΔCDH~ΔCFB

=>\(\dfrac{CD}{CF}=\dfrac{CH}{CB}\)

=>\(CD\cdot CB=CH\cdot CF\)

\(BF\cdot BA+CH\cdot CF=BD\cdot BC+CD\cdot CB=BC\left(BD+CD\right)=BC^2\)

Answer 2