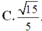Question

Ai đó làm ơn giúp mình câu này với ạ Cho hình trụ ABC.A'B'C' có đáy là tam giác ABC cân tại A, góc BAC bằng 120° và AB=2a. Hình chiếu của A' trên mặt phẳng (ABC) trùng với trung điểm H của BC, biết AA' =a√2. Tính góc giữa đường thẳng AA' và mặt phẳng (ABC)

Answer 1

Vì A'H⊥(ABC)

nên \(\hat{A^{\prime}A;\left(ABC\right)}=\hat{A^{\prime}A;AH}=\hat{A^{\prime}AH}\)

Vì A'H⊥(ABC)

nên A'H⊥HA

=>ΔHA'A vuông tại H

ΔABC cân tại A

=>\(\hat{ABC}=\hat{ACB}=\frac{180^0-\hat{BAC}}{2}=\frac{180^0-120^0}{2}=30^0\)

ΔABC cân tại A

mà AH là đường trung tuyến

nên AH⊥BC

Xét ΔAHB vuông tại H có \(\sin B=\frac{AH}{AB}\)

=>\(\frac{AH}{2a}=\sin30=\frac12\)

=>AH=a

Xét ΔA'HA vuông tại H có cos HAA'=\(\frac{AH}{A^{\prime}A}=\frac{a}{a\sqrt2}=\frac{1}{\sqrt2}\)

nên \(\hat{A^{\prime}AH}=45^0\)

=>\(\hat{A^{\prime}A;\left(ABC\right)}=45^0\)