Question

Câu 13. Tính diện tích \( S \) của hình phẳng được gạch chéo ở trong Hình.

Answer 1

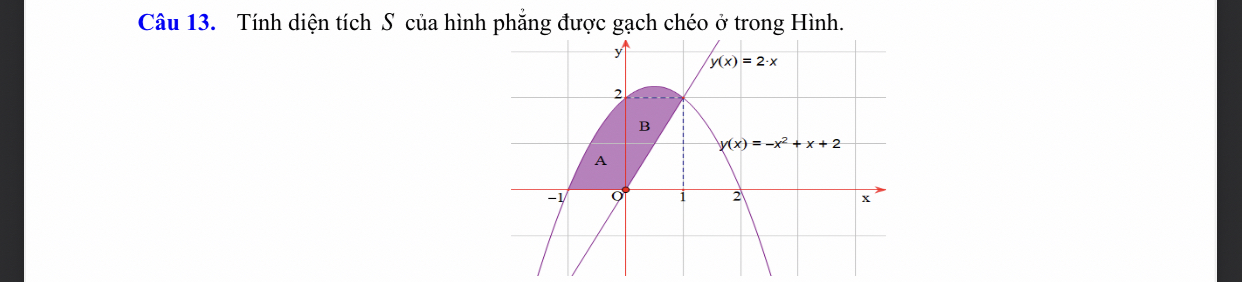
Diện tích giao 2 đồ thị \(y=2x;y=-x^2+x+2\) với \(x\in\left[-1;1\right]\)

\(S'=\int\limits^{-1}_1\left(-x^2+x+2-2x\right)dx\)

\(\Rightarrow S'=\int\limits^{-1}_1\left(-x^2-x+2\right)dx\)

\(\Rightarrow S'=\left[\dfrac{x^3}{3}-\dfrac{x^2}{2}+2x\right]^{-1}_1=\dfrac{13}{6}+\dfrac{7}{6}=\dfrac{20}{6}=\dfrac{10}{3}\left(đvdt\right)\)

Theo đồ thị ta được :

\(S=S'-S_{\Delta}=\dfrac{10}{3}-\dfrac{1}{2}.1.2=\dfrac{7}{3}\left(đvdt\right)\)