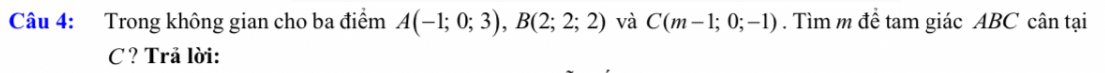\(AC=\sqrt{\left(m-1+1\right)^2+\left(0-0\right)^2+\left(-1-3\right)^2}=\sqrt{m^2+16}\)
\(BC=\sqrt{\left(m-1-2\right)^2+\left(0-2\right)^2+\left(-1-2\right)^2}=\sqrt{\left(m-3\right)^2+13}=\sqrt{m^2-6m+22}\)
Để \(\Delta ABC\) cân tại \(C\) khi và chỉ khi
\(\Leftrightarrow AC=BC\)
\(\Leftrightarrow\sqrt{m^2+16}=\sqrt{m^2-6m+22}\)
\(\Leftrightarrow m^2+16=m^2-6m+22\left(m^2+16>0\right)\)
\(\Leftrightarrow6m=6\)
\(\Leftrightarrow m=1\)
Vậy \(m=1\) thỏa mãn đề bài
Đúng 1
Bình luận (0)
