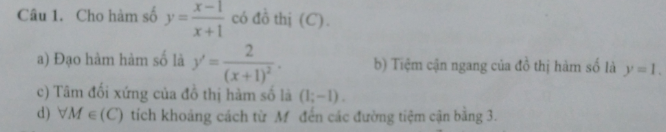a) \(y'=\dfrac{1-1.\left(-1\right)}{\left(x+1\right)^2}=\dfrac{2}{\left(x+1\right)^2}\Rightarrow\) Đúng
b) \(\lim\limits_{x\rightarrow\infty}\dfrac{x-1}{x+1}=1\Rightarrow TCN:y=1\Rightarrow\) Đúng
c) \(\lim\limits_{x\rightarrow-1}\dfrac{x-1}{x+1}=\infty\Rightarrow TCĐ:x=-1\)
Tâm đối xứng \(I\) của Hs là giao điểm của TCĐ và TCN
\(\Rightarrow I\left(-1;1\right)\Rightarrow\) Sai
d) \(d\left(M;TXĐ\right)=\left|x+1\right|\)
\(d\left(M;TCN\right)=\left|y-1\right|=\left|\dfrac{x-1}{x+1}-1\right|=\dfrac{2}{\left|x+1\right|}\)
\(\Rightarrow d\left(M;TCĐ\right).d\left(M;TCN\right)=\left|x+1\right|.\dfrac{2}{\left|x+1\right|}=2\ne3\)
\(\Rightarrow\) Sai