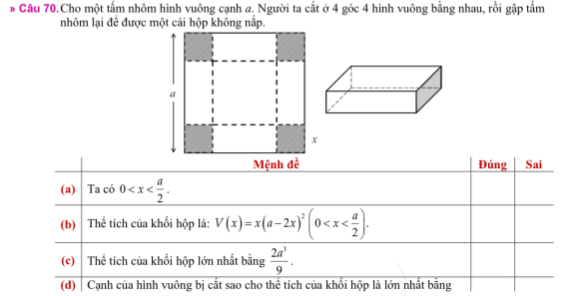
a) Đúng (vì khi \(x>\dfrac{a}{2}\) thì không tạo được cái hộp không nắp)
b) \(V\left(x\right)=\left(a-2x\right)^2x\Rightarrow\) Đúng
c) \(V'\left(x\right)=\left(a-2x\right)^2-4x\left(a-2x\right)=\left(a-2x\right)\left(a-6x\right)\)
\(V'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{a}{2}\\x=\dfrac{a}{6}\end{matrix}\right.\)
Lập bảng biến thiên ta được :
\(V\left(x\right)\) đồng biến trên \(\left(-\infty;\dfrac{a}{6}\right)\cup\left(\dfrac{a}{2};+\infty\right)\) và nghịch biến trên \(\left(\dfrac{a}{6};\dfrac{a}{2}\right)\)
Nên \(V\left(x\right)_{max}=V\left(\dfrac{a}{6}\right)==\left(a-\dfrac{a}{3}\right)^2.\dfrac{a}{6}=\dfrac{2a^2}{27}\)
\(\Rightarrow\) Sai
c) \(V\left(x\right)_{max}=\dfrac{2a^3}{27}\left(đơn.vị.thể.tích\right)\) (do đánh nhầm)
Còn câu d không biết cạnh hình vuông là bao nhiêu?