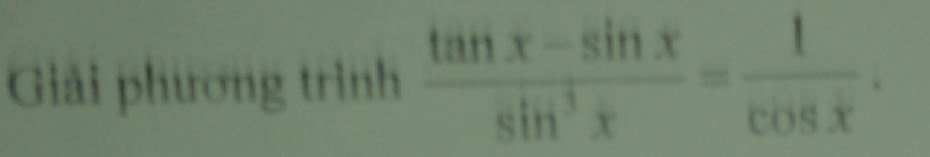\(\dfrac{tanx-sinx}{sin^3x}=\dfrac{1}{cosx}\left(1\right)\left(sinx\ne0;cosx\ne0\right)\)
\(VT=\dfrac{tanx-sinx}{sin^3x}=\dfrac{\dfrac{sinx}{cosx}-sinx}{sin^3x}=\dfrac{sinx\left(1-cosx\right)}{sin^3x.cosx}=\dfrac{1-cosx}{sin^2x.cosx}\)
\(=\dfrac{1-cosx}{\left(1-cos^2x\right).cosx}=\dfrac{1}{\left(1+cosx\right)cosx}\)
\(\left(1\right)\Rightarrow\dfrac{1}{1+cosx}=1\)
\(\Leftrightarrow cosx=-1\)
\(\Leftrightarrow x=\pi+k2\pi\left(k\in Z\right)\) so với điều kiện \(sinx\ne0\Leftrightarrow x\ne k\pi\) không thỏa
Vậy phương trình cho vô nghiệm
Đúng 1
Bình luận (0)
