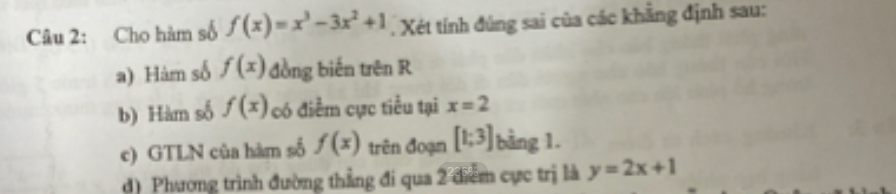a) \(y'=3x^2-6x=3x\left(x-2\right)\)
\(y'=0\Leftrightarrow x=0;x=2\)
HS đồng biến trên \(\left(-\infty;0\right)\cup\left(2;+\infty\right)\) và nghịch biến trên \(\left(0;2\right)\)
\(\Rightarrow\) Sai
b) Theo sự biến thiên như trên \(f\left(x\right)_{min}\) tại \(x=2\)
\(\Rightarrow\) Đúng
c) \(f\left(1\right)=-1;f\left(2\right)=-3;f\left(3\right)=1\)
\(\Rightarrow\) HS có \(GTLN=1\) tại \(x=3\in\left[1;3\right]\)
\(\Rightarrow\) Đúng
d) Tọa độ 2 điểm cực trị của HS là \(\left(0;1\right)\&\left(2;-3\right)\)
Phương trình đường thẳng qua 2 điểm cực trị là :
\(\dfrac{y-1}{x-0}=\dfrac{-3-1}{2-0}\)
\(\Leftrightarrow y=-2x+1\)
\(\Rightarrow\) Sai