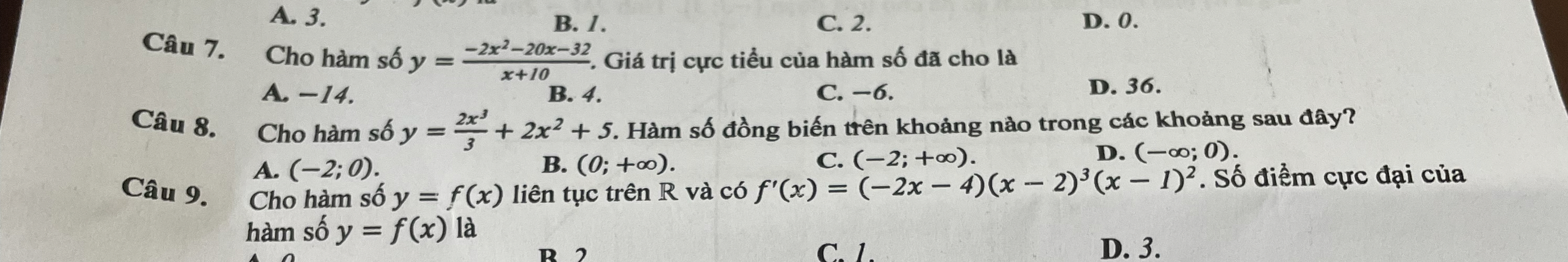Câu 7 : \(y'=\dfrac{-2x^2-40x-168}{\left(x+10\right)^2}\)
\(y'=0\Leftrightarrow-2x^2-40x-168=0\Leftrightarrow x=-6\cup x=-14\)
Lập BTT đồ thị HS đạt cực tiểu tại \(x=-14\Rightarrow y_{min}=36\)
Vậy chọn D
Câu 8 : \(y'=2x^2+4x\)
\(y'>0\Leftrightarrow2x^2+4x>0\Leftrightarrow2x\left(x+2\right)>0\Leftrightarrow x\in\left(-\infty;-2\right)\cup\left(0;+\infty\right)\)
Vậy chọn B
Câu 9 : \(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\\x=2\end{matrix}\right.\)
Lập bảng biến thiên ta được HS đạt cực đại tại \(x=1\)
Vậy chọn C
9.
Hàm có 2 điểm cực trị là \(x=-2;x=2\) (\(x=1\) ko phải cực trị)
Do đó hàm số có 1 cực đại và 1 cực tiểu