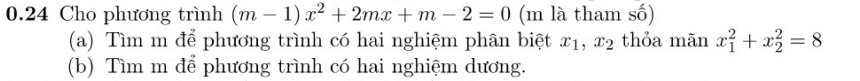\(\left(m-1\right)x^2+2mx+m-2=0\left(1\right)\)
a) Để (1) có 2 nghiệm phân biệt khi và chỉ khi
\(\Delta'=m^2-\left(m-2\right)\left(m-1\right)>0\) và \(m\ne1\)
\(\Leftrightarrow m^2-m^2+3m-2>0\)
\(\Leftrightarrow m>\dfrac{2}{3}\)\(\)
\(x_1^2+x_2^2=8\Leftrightarrow S^2-2P=8\)
\(\Leftrightarrow\left(-\dfrac{2m}{m-1}\right)^2-2\dfrac{m-2}{m-1}=8\)
\(\Leftrightarrow4m^2-2\left(m-1\right)\left(m-2\right)=8\left(m-1\right)^2\)
\(\Leftrightarrow4m^2-2m^2+6m-4=8m^2-16m+8\)
\(\Leftrightarrow6m^2-22m+12=0\) hay \(3m^2-11m+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{2}{3}\left(ktm\right)\\m=3\end{matrix}\right.\)
Vậy \(m=3\) thỏa mãn đề bài