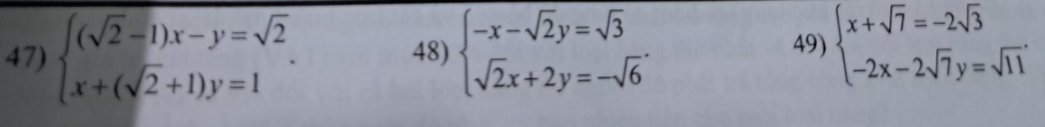\(\left\{{}\begin{matrix}\left(\sqrt{2}-1\right)x-y=\sqrt{2}\\x+\left(\sqrt{2}+1\right)y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)x-\left(\sqrt{2}+1\right)y=\sqrt{2}\left(\sqrt{2}+1\right)\\x+\left(\sqrt{2}+1\right)y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-\left(\sqrt{2}+1\right)y=2+\sqrt[]{2}\\x+\left(\sqrt{2}+1\right)y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=3+\sqrt{2}\\x+\left(\sqrt{2}+1\right)y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3+\sqrt{2}}{2}\\\left(\sqrt{2}+1\right)y=1-x=\dfrac{2-3-\sqrt{2}}{2}=\dfrac{-1-\sqrt{2}}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3+\sqrt{2}}{2}\\y=\dfrac{-\left(\sqrt{2}+1\right)}{2}:\left(\sqrt{2}+1\right)=-\dfrac{1}{2}\end{matrix}\right.\)
47: \(\left\{{}\begin{matrix}x\left(\sqrt{2}-1\right)-y=\sqrt{2}\\x+\left(\sqrt{2}+1\right)y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(\sqrt{2}-1\right)-y=\sqrt{2}\\x\left(\sqrt{2}-1\right)+y=\sqrt{2}-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(\sqrt{2}-1\right)-y+x\left(\sqrt{2}-1\right)+y=2\sqrt{2}-1\\x\left(\sqrt{2}-1\right)-y=\sqrt{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(2\sqrt{2}-2\right)=2\sqrt{2}-1\\y=x\left(\sqrt{2}-1\right)-\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2\sqrt{2}-1}{2\sqrt{2}-2}=\dfrac{3+\sqrt{2}}{2}\\y=\dfrac{\left(3+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{2}-\sqrt{2}=-\dfrac{1}{2}\end{matrix}\right.\)
48: \(\left\{{}\begin{matrix}-x-y\sqrt{2}=\sqrt{3}\\\sqrt{2}x+2y=-\sqrt{6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x\sqrt{2}-2y=\sqrt{6}\\x\sqrt{2}+2y=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x\sqrt{2}-2y+x\sqrt{2}+2y=0\\-x-y\sqrt{2}=\sqrt{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0y=0\\-x=y\sqrt{2}+\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in R\\x=-y\sqrt{2}-\sqrt{3}\end{matrix}\right.\)
49: \(\left\{{}\begin{matrix}x+\sqrt{7}=-2\sqrt{3}\\-2x-2\sqrt{7}y=\sqrt{11}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\sqrt{3}-\sqrt{7}\\2\sqrt{7}\cdot y=-2x-\sqrt{11}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\sqrt{3}-\sqrt{7}\\y\cdot2\sqrt{7}=-2\left(-2\sqrt{3}-\sqrt{7}\right)-\sqrt{11}=4\sqrt{3}+2\sqrt{7}-\sqrt{11}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\sqrt{3}-\sqrt{7}\\y=\dfrac{4\sqrt{3}+2\sqrt{7}-\sqrt{11}}{2\sqrt{7}}=\dfrac{4\sqrt{21}+14-\sqrt{77}}{14}\end{matrix}\right.\)