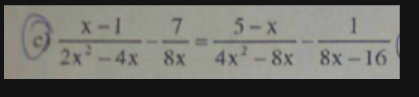ĐKXĐ: \(x\notin\left\{0;2\right\}\)
\(\dfrac{x-1}{2x^2-4x}-\dfrac{7}{8x}=\dfrac{5-x}{4x^2-8x}-\dfrac{1}{8x-16}\)
=>\(\dfrac{x-1}{2x\left(x-2\right)}-\dfrac{7}{8x}=\dfrac{5-x}{4x\left(x-2\right)}-\dfrac{1}{8\left(x-2\right)}\)
=>\(\dfrac{4\left(x-1\right)}{8x\left(x-2\right)}-\dfrac{7\left(x-2\right)}{8x\left(x-2\right)}=\dfrac{2\left(5-x\right)}{8x\left(x-2\right)}-\dfrac{x}{8x\left(x-2\right)}\)
=>4(x-1)-7(x-2)=2(5-x)-x
=>4x-4-7x+14=10-2x-x
=>-3x+10=-3x+10
=>0x=0(luôn đúng)
Vậy: \(x\in R\backslash\left\{0;2\right\}\)
\(\dfrac{x-1}{2x^2-4x}-\dfrac{7}{8x}=\dfrac{5-x}{4x^2-8x}-\dfrac{1}{8x-16}\left(x\ne0;x\ne2\right)\\ \Leftrightarrow\dfrac{x-1}{2x\left(x-2\right)}-\dfrac{7}{8x}=\dfrac{5-x}{4x\left(x-2\right)}-\dfrac{1}{8\left(x-2\right)}\\ \Leftrightarrow\dfrac{4\left(x-1\right)}{8x\left(x-2\right)}-\dfrac{7\left(x-2\right)}{8x\left(x-2\right)}=\dfrac{2\left(5-x\right)}{8x\left(x-2\right)}-\dfrac{x}{8x\left(x-2\right)}\\ \Leftrightarrow4\left(x-1\right)-7\left(x-2\right)=2\left(5-x\right)-x\\ \Leftrightarrow4x-4-7x+14=10-2x-x\\ \Leftrightarrow-3x+10=10-3x\\ \Leftrightarrow0x=0\)
=> Pt vô số nghiệm khi x khác 0 và 2