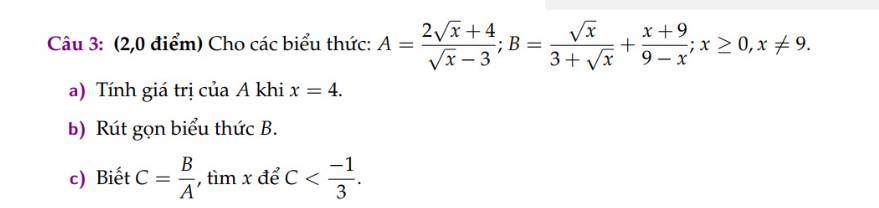a) Thay x=4 vào A ta có:
\(A=\dfrac{2\sqrt{4}+4}{\sqrt{4}-3}=\dfrac{2\cdot2+4}{2-3}=\dfrac{8}{-1}=-8\)
b) \(B=\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{x+9}{x-9}\)
\(B=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{x-3\sqrt{x}-x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{-3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(B=\dfrac{-3}{\sqrt{x}-3}\)
c) Ta có: \(C=\dfrac{B}{A}\)
\(C=\dfrac{-3}{\sqrt{x}-3}:\dfrac{2\sqrt{x}+4}{\sqrt{x}-3}\)
\(C=\dfrac{-3}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{2\sqrt{x}+4}\)
\(C=\dfrac{-3}{2\sqrt{x}+4}\)
Mà: \(C< -\dfrac{1}{3}\) khi:
\(\dfrac{-3}{2\sqrt{x}+4}< -\dfrac{1}{3}\)
\(\Rightarrow\dfrac{-3\cdot3}{2\left(\sqrt{x}+2\right)\cdot3}+\dfrac{2\sqrt{x}+4}{3\cdot2\left(\sqrt{x}+2\right)}< 0\)
\(\Rightarrow\dfrac{2\sqrt{x}+4-9}{6\left(\sqrt{x}+2\right)}< 0\)
\(\Rightarrow\dfrac{2\sqrt{x}-5}{6\left(\sqrt{x}+2\right)}< 0\)
Mà: \(6\left(\sqrt{x}+2\right)>0\)
\(\Rightarrow2\sqrt{x}-5< 0\)
\(\Rightarrow2\sqrt{x}< 5\)
\(\Rightarrow x< \dfrac{25}{4}\)
\(\Rightarrow0\le x< \dfrac{25}{4}\)
a) \(A=\dfrac{2\sqrt{x}+4}{\sqrt{x}-3}\left(x\ge0;x\ne9\right)\)
Thay \(x=4\) vào \(A\), ta được:
\(A=\dfrac{2\sqrt{4}+4}{\sqrt{4}-3}=\dfrac{4+4}{2-3}=-8\)
b) \(B=\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\left(x\ge0;x\ne9\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}-x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{-3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{-3}{\sqrt{x}-3}\)
c) \(C=\dfrac{B}{A}\)
\(=\dfrac{-3}{\sqrt{x}-3}:\dfrac{2\sqrt{x}+4}{\sqrt{x}-3}\)
\(=\dfrac{-3}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{2\sqrt{x}+4}\)
\(=\dfrac{-3}{2\sqrt{x}+4}\)
Khi đó: \(C< \dfrac{-1}{3}\)
\(\Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}< \dfrac{-1}{3}\)
\(\Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+\dfrac{1}{3}< 0\)
\(\Leftrightarrow\dfrac{-9}{3\left(2\sqrt{x}+4\right)}+\dfrac{2\sqrt{x}+4}{3\left(2\sqrt{x}+4\right)}< 0\)
\(\Leftrightarrow\dfrac{-9+2\sqrt{x}+4}{6\sqrt{x}+12}< 0\)
\(\Leftrightarrow2\sqrt{x}-5< 0\left(vì.6\sqrt{x}+12>0\right)\)
\(\Leftrightarrow2\sqrt{x}< 5\)
\(\Leftrightarrow\sqrt{x}< \dfrac{5}{2}\)
\(\Leftrightarrow x< \dfrac{25}{4}\)
Kết hợp với điều kiện của \(x\), ta được:
\(0\le x< \dfrac{25}{4}\)
\(Toru\)