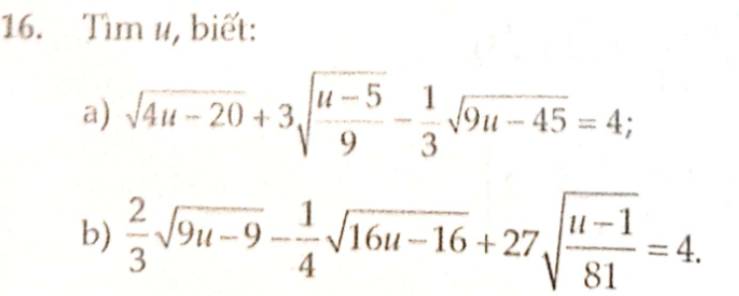a) \(\sqrt{4u-20}+3\sqrt{\dfrac{u-5}{9}}-\dfrac{1}{3}\sqrt{9u-45}=4\) (ĐK: \(u\ge5\))
\(\Leftrightarrow\sqrt{4\left(u-5\right)}+\dfrac{3\sqrt{u-5}}{3}-\dfrac{1}{3}\sqrt{9\left(u-5\right)}=4\)
\(\Leftrightarrow2\sqrt{u-5}+\sqrt{u-5}-\dfrac{1}{3}\cdot3\sqrt{u-5}=4\)
\(\Leftrightarrow2\sqrt{u-5}+\sqrt{u-5}-\sqrt{u-5}=4\)
\(\Leftrightarrow2\sqrt{u-5}=4\)
\(\Leftrightarrow\sqrt{u-5}=2\)
\(\Leftrightarrow u-5=2^2\)
\(\Leftrightarrow u=4+5\)
\(\Leftrightarrow u=9\left(tm\right)\)
b) \(\dfrac{2}{3}\sqrt{9u-9}-\dfrac{1}{4}\sqrt{16u-16}+27\sqrt{\dfrac{u-1}{81}}=4\) (ĐK: \(u\ge1\))
\(\Leftrightarrow\dfrac{2}{3}\sqrt{9\left(u-1\right)}-\dfrac{1}{4}\sqrt{16\left(u-1\right)}+\dfrac{27\sqrt{u-1}}{\sqrt{81}}=4\)
\(\Leftrightarrow\dfrac{2}{3}\cdot3\sqrt{u-1}-\dfrac{1}{4}\cdot4\sqrt{u-1}+27\cdot\dfrac{\sqrt{u-1}}{9}=4\)
\(\Leftrightarrow2\sqrt{u-1}-\sqrt{u-1}+3\sqrt{u-1}=4\)
\(\Leftrightarrow4\sqrt{u-1}=4\)
\(\Leftrightarrow\sqrt{u-1}=1\)
\(\Leftrightarrow u-1=1\)
\(\Leftrightarrow u=1+1\)
\(\Leftrightarrow u=2\left(tm\right)\)
a: \(\Leftrightarrow2\sqrt{u-5}+3\cdot\dfrac{\sqrt{u-5}}{3}-\dfrac{1}{3}\cdot3\sqrt{u-5}=4\)
=>\(2\cdot\sqrt{u-5}=4\)
=>u-5=4
=>u=9
b: \(\Leftrightarrow3\sqrt{u-1}\cdot\dfrac{2}{3}-\dfrac{1}{4}\cdot4\sqrt{u-1}+27\cdot\dfrac{\sqrt{u-1}}{9}=4\)
=>\(4\sqrt{u-1}=4\)
=>u-1=1
=>u=2