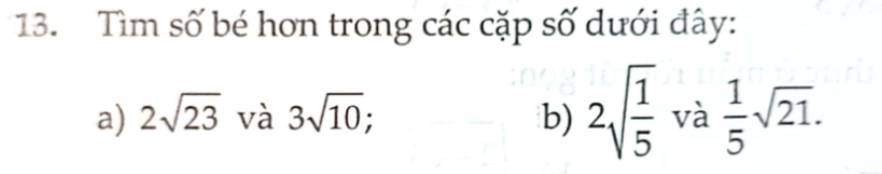a) Ta có:
\(2\sqrt{23}=\sqrt{2^2\cdot23}=\sqrt{4\cdot23}=\sqrt{92}\)
\(3\sqrt{10}=\sqrt{3^2\cdot10}=\sqrt{9\cdot10}=\sqrt{90}\)
Mà:
\(92>90\)
\(\Rightarrow\sqrt{92}>\sqrt{90}\)
\(\Rightarrow2\sqrt{23}>3\sqrt{10}\)
Vậy số lớn hơn là: \(2\sqrt{23}\)
b) Ta có:
\(2\sqrt{\dfrac{1}{5}}=\sqrt{2^2\cdot\dfrac{1}{5}}=\sqrt{4\cdot\dfrac{1}{5}}=\sqrt{\dfrac{4}{5}}=\sqrt{0,8}\)
\(\dfrac{1}{5}\cdot\sqrt{21}=\sqrt{\left(\dfrac{1}{5}\right)^2\cdot21}=\sqrt{\dfrac{21}{25}}=\sqrt{0,84}\)
Mà: \(0,8< 0,84\)
\(\Rightarrow\sqrt{0,8}< \sqrt{0,84}\)
\(\Rightarrow2\sqrt{\dfrac{1}{5}}< \dfrac{1}{5}\sqrt{21}\)
Vậy số lớn hơn là: \(\dfrac{1}{5}\sqrt{21}\)
a: \(2\sqrt{23}=\sqrt{4\cdot23}=\sqrt{92}\)
\(3\sqrt{10}=\sqrt{9\cdot10}=\sqrt{90}\)
mà 92>90
nên \(2\sqrt{23}\) là số lớn hơn
b: \(2\sqrt{\dfrac{1}{5}}=\sqrt{2^2\cdot\dfrac{1}{5}}=\sqrt{\dfrac{4}{5}}=\sqrt{0.8}\)
\(\dfrac{1}{5}\sqrt{21}=\sqrt{21\cdot\dfrac{1}{25}}=\sqrt{0.84}\)
mà 0,8<0,84
nên \(\dfrac{1}{5}\sqrt{21}\) là số lớn hơn