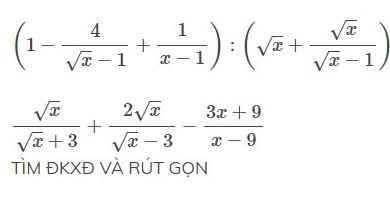\(\left(1-\dfrac{4}{\sqrt{x}-1}+\dfrac{1}{x-1}\right):\left(\sqrt{x}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\right)\left(dkxd:x\ge0,x\ne1\right)\\ =\left(1-\dfrac{4}{\sqrt{x}-1}+\dfrac{1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}}{\sqrt{x}-1}\right)\\ =\dfrac{x-1-4\left(\sqrt{x}+1\right)+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{x-\sqrt{x}+\sqrt{x}}\\ =\dfrac{x-1-4\sqrt{x}-4+1}{\sqrt{x}+1}.\dfrac{1}{x}\\ =\dfrac{x-4\sqrt{x}-4}{x\left(\sqrt{x}+1\right)}=\dfrac{x-4\sqrt{x}-4}{x\sqrt{x}+x}\)
\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\left(dkxd:x\ge0,x\ne9\right)\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-\left(3x+9\right)}{x-9}\\ =\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}\\ =\dfrac{3\sqrt{x}-9}{x-9}\\ =\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{3}{\sqrt{x}+3}\)
\(\left(1-\dfrac{4}{\sqrt{x}-1}+\dfrac{1}{x-1}\right):\left(\sqrt{x}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\right)\) (ĐK: \(x\ge0,x\ne1\))
\(=\left[\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{4\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\right]\)
\(=\dfrac{x-1-4\sqrt{x}-4+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{x-\sqrt{x}+\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{x-4\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{x}\)
\(=\dfrac{x-4\sqrt{x}-4}{x\left(\sqrt{x}+1\right)}\)
Bài dưới mình làm rồi nhé !