1) \(P=\dfrac{2x+2}{\sqrt{x}}+\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x^2+\sqrt{x}}{x\sqrt{x}+x}\)
\(P=\dfrac{2x+2}{\sqrt{x}}+\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}\left(x\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{2x+2}{\sqrt{x}}+\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(P=\dfrac{2x+2+x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\)
\(P=\dfrac{3x+\sqrt{x}+3-x+\sqrt{x}-1}{\sqrt{x}}\)
\(P=\dfrac{2x+2\sqrt{x}+2}{\sqrt{x}}\)
2) Ta có:
\(x=3-2\sqrt{2}=\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2=\left(\sqrt{2}-1\right)^2\)
Thay vào P ta có:
\(P=\dfrac{2\left(\sqrt{2}-1\right)^2+2\sqrt{\left(\sqrt{2}-1\right)^2}+2}{\sqrt{\left(\sqrt{2}-1\right)^2}}=6\)
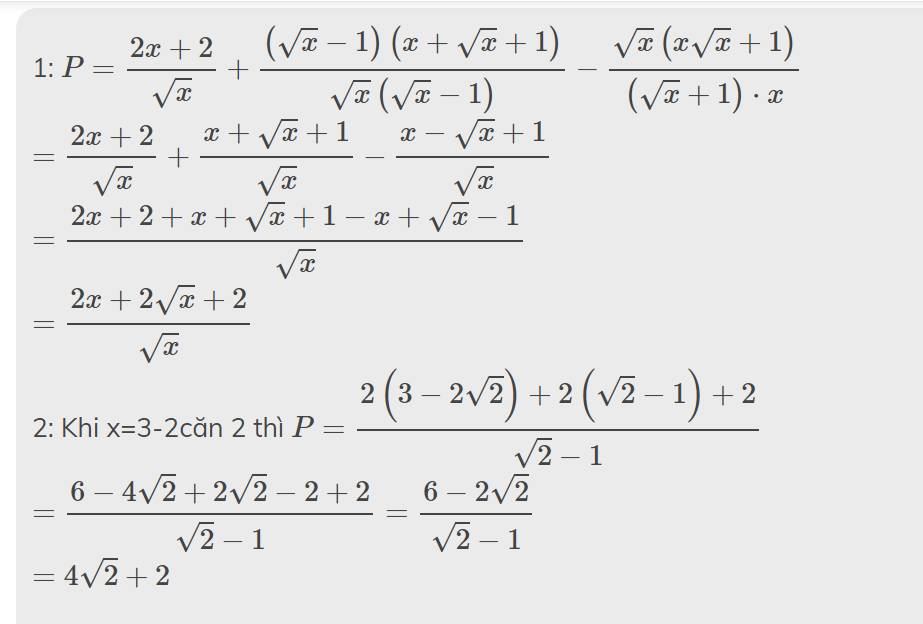
3:
\(A=\dfrac{7}{P}=7:\dfrac{2x+2\sqrt{x}+2}{\sqrt{x}}=\dfrac{7\sqrt{x}}{2x+2\sqrt{x}+2}>0\)
Đặt A=1
=>\(2x+2\sqrt{x}+2=7\sqrt{x}\)
=>\(2x-5\sqrt{x}+2=0\)
=>\(\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
=>x=4(nhận) hoặc x=1/2(nhận)
Nếu A>=2 thì ta sẽ có:
\(a\left(2x+2\sqrt{x}+2\right)=7\sqrt{x}\)(a>=2, a nguyên)
=>\(2xa+2\sqrt{x}a+2a-7\sqrt{x}=0\)(1)
Đặt \(\sqrt{x}=b\left(b>=0\right)\)
(1) sẽ trở thành 2ab^2+2ab+2a-7b=0
=>2ab^2+b(2a-7)+2a=0
Δ=(2a-7)^2-4*2a*2a
=4a^2-28a+49-16a
=4a^2-44a+49
Để PT có nghiệm thì 4a^2-44a+49>=0
=>\(a>=\dfrac{11+6\sqrt{2}}{2}\simeq9,74\) hoặc \(a< =\dfrac{11-6\sqrt{2}}{2}\simeq1,25\left(loại\right)\)
=>a>=10
Nhưng để b thỏa mãn điều kiện b>=0 thì cần thêm như sau:
\(\left\{{}\begin{matrix}a>=10\\\left[{}\begin{matrix}2a\cdot2a< =0\\\left\{{}\begin{matrix}\dfrac{-2a+7}{2a}>=0\\\dfrac{2a}{2a}>=0\left(đúng\right)\end{matrix}\right.\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a>=10\\\left[{}\begin{matrix}0< =a< =\dfrac{7}{2}\\a=0\end{matrix}\right.\end{matrix}\right.\)(vô lý)
=>A chỉ có 1 giá trị nguyên duy nhất là 1 mà thôi















