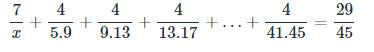\(\dfrac{7}{x}+\dfrac{4}{5.9}+\dfrac{4}{9.13}+\dfrac{4}{13.17}+...+\dfrac{4}{41.45}=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{17}+...+\dfrac{1}{37}-\dfrac{1}{41}+\dfrac{1}{41}-\dfrac{1}{45}=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\dfrac{1}{5}-\dfrac{1}{45}=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\dfrac{8}{45}=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}=\dfrac{29}{45}-\dfrac{8}{45}=\dfrac{7}{15}\)
\(\Leftrightarrow x=15\)
=>\(\dfrac{7}{x}+\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+...+\dfrac{1}{41}-\dfrac{1}{45}\right)=\dfrac{29}{45}\)
=>7/x+1/5-1/45=29/45
=>7/x+8/45=29/45
=>7/x=21/45
=>7/x=7/15
=>x=15
\(\dfrac{7}{x}+\dfrac{4}{5\cdot9}+\dfrac{4}{9\cdot13}+...+\dfrac{4}{41\cdot45}=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\left(\dfrac{4}{5\cdot9}+\dfrac{4}{9\cdot13}+...+\dfrac{4}{41\cdot45}\right)=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+...+\dfrac{1}{41}-\dfrac{1}{45}\right)=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\left(\dfrac{1}{5}-\dfrac{1}{45}\right)=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}+\dfrac{8}{45}=\dfrac{29}{45}\)
\(\Rightarrow\dfrac{7}{x}=\dfrac{29}{45}-\dfrac{8}{45}\)
\(\Rightarrow\dfrac{7}{x}=\dfrac{21}{45}\)
\(\Rightarrow\dfrac{7}{x}=\dfrac{7}{15}\)
\(\Rightarrow x=15\)