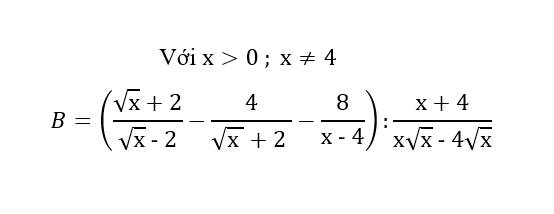\(=\dfrac{x+4\sqrt{x}+4-4\sqrt{x}+8-8}{x-4}\cdot\dfrac{\sqrt{x}\left(x-4\right)}{x+4}\)
\(=\dfrac{x+4}{x+4}\cdot\sqrt{x}=\sqrt{x}\)
Với mọi \(x>0\) và \(x\ne4\), ta có :
\(B=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{4}{\sqrt{x}+2}-\dfrac{8}{x-4}\right):\dfrac{x+4}{x\sqrt{x}-4\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+2\right)^2-4\left(\sqrt{x}-2\right)-8}{x-4}:\dfrac{x+4}{\sqrt{x}\left(x-4\right)}\)
\(=\dfrac{x+4\sqrt{x}+4-4\sqrt{x}+8-8}{x-4}\cdot\dfrac{\sqrt{x}\left(x-4\right)}{x+4}\)
\(=\dfrac{x+4}{x-4}\cdot\dfrac{\sqrt{x}\left(x-4\right)}{x+4}=\sqrt{x}\).
Vậy : Với mọi \(x>0,x\ne4\) thì \(B=\sqrt{x}\).