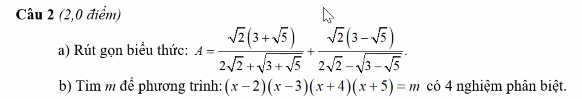a: \(=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{6+2\sqrt{5}}}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{2\left(3+\sqrt{5}\right)}{4+\sqrt{5}+1}+\dfrac{2\left(3-\sqrt{5}\right)}{4-\sqrt{5}+1}\)
\(=\dfrac{\left(\sqrt{5}+1\right)^2}{\sqrt{5}\left(\sqrt{5}+1\right)}+\dfrac{\left(\sqrt{5}-1\right)^2}{\sqrt{5}\left(\sqrt{5}-1\right)}\)
\(=\dfrac{\sqrt{5}+1+\sqrt{5}-1}{\sqrt{5}}=2\)
b: (x-2)(x-3)(x+4)(x+5)=m
=>(x^2+2x-8)(x^2+2x-15)=m
=>(x^2+2x)^2-23(x^2+2x)+120-m=0
Để phương trình có 4 nghiệm phân biệt thì
(-23)^2-4(120-m)>0 và 120-m>0
=>529-480+4m>0 và m<120
=>m>-49/4 và m<120
Đúng 0
Bình luận (0)
