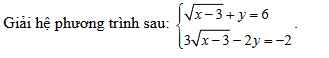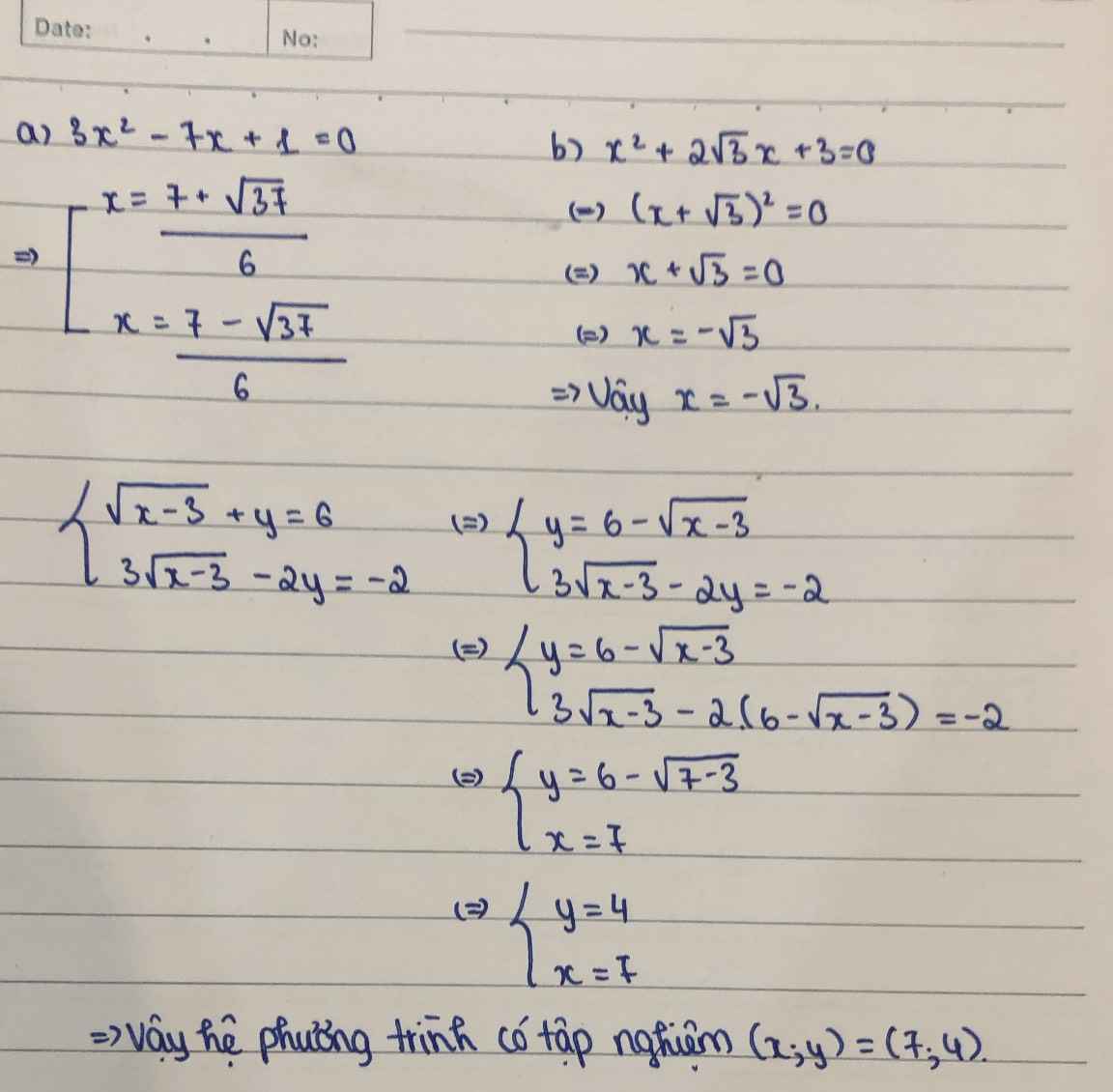a: 
b: \(\Leftrightarrow\left(x+\sqrt{3}\right)^2=0\)
\(\Leftrightarrow x+\sqrt{3}=0\)
hay \(x=-\sqrt{3}\)
a.\(3x^2-7x+1=0\)
\(\Delta=\left(-7\right)^2-4.3.1=49-12=37\)
=> pt có 2 nghiệm:
\(\left\{{}\begin{matrix}x=\dfrac{7+\sqrt{37}}{6}\\x=\dfrac{7-\sqrt{37}}{6}\end{matrix}\right.\)
b.\(x^2+2\sqrt{3}x+3=0\)
\(\Leftrightarrow\left(x+\sqrt{3}\right)^2=0\)
\(\Leftrightarrow x+\sqrt{3}=0\Leftrightarrow x=-\sqrt{3}\)
hpt: \(\left\{{}\begin{matrix}\sqrt{x-3}+y=6\\3\sqrt{x-3}-2y=-2\end{matrix}\right.\)
\(ĐK:x\ge3\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x-3}+2y=12\\3\sqrt{x-3}-2y=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x-3}=10\\3\sqrt{x-3}-2y=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-3}=2\\3.2-2y=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x-3=4\\-2y=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=4\end{matrix}\right.\)
ĐKXĐ:\(x\ge3\)
\(\left\{{}\begin{matrix}\sqrt{x-3}+y=6\\3\sqrt{x-3}-2y=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-2\sqrt{x-3}-2y=-12\\3\sqrt{x-3}-2y=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-3}+y=6\\5\sqrt{x-3}=10\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2+y=6\\\sqrt{x-3}=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x-3=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x=7\left(tm\right)\end{matrix}\right.\)