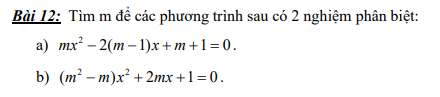a: Để đây là ptb2 thì m<>0
\(\text{Δ}=\left(2m-2\right)^2-4m\left(m+1\right)\)
\(=4m^2-8m+4-4m^2-4m\)
=-12m+4
Để phương trình có hai nghiệm phân biệt thì -12m+4>0
=>-12m>-4
hay m<1/3
=>m<1/3 và m<>0
b: Để đây là ptb2 thì m(m-1)<>0
hay \(m\notin\left\{0;1\right\}\)
\(\text{Δ}=\left(2m\right)^2-4\left(m^2-m\right)=4m^2-4m^2+4m=4m\)
Để phương trình có hai nghiệm phân biệt thì 4m>0
hay m>0
=>m>0 và m<>1
a, Để pt có nghiệm phân biệt thì \(\Delta'>0\)
\(\Rightarrow\left[-\left(m-1\right)\right]^2-m\left(m+1\right)>0\\ \Rightarrow m^2-2m+1-m^2-m>0\\ \Rightarrow-3m+1>0\\ \Rightarrow-3m>-1\\ \Rightarrow m< \dfrac{1}{3}\)
a, Để pt có nghiệm phân biệt thì \(\Delta'>0\)
\(\Rightarrow m^2-\left(m^2-m\right).1>0\\ \Rightarrow m^2-m^2+m>0\\ \Rightarrow m>0\)