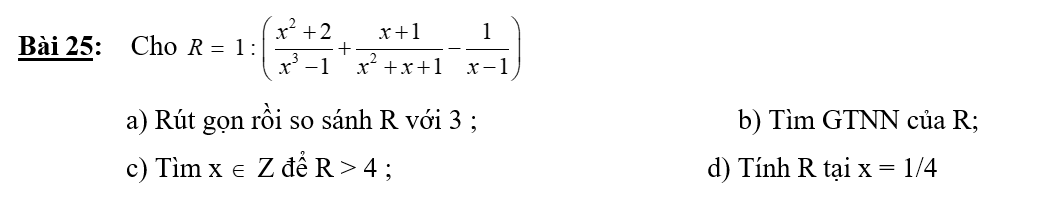a) \(R=1:\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)=1:\left(\dfrac{x^2+2+\left(x+1\right)\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\right)=1.\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x^2+2+x^2-1-x^2-x-1}=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x^2-x}=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}=\dfrac{x^2+x+1}{x}\)
\(R=\dfrac{x^2+x+1}{x}=x+1+\dfrac{1}{x}\ge2\sqrt{x.\dfrac{1}{x}}+1=3\)( bất đẳng thức Cauchy cho 2 số dương)
a) ĐKXĐ: \(\left\{{}\begin{matrix}x^3-1\ne0\\x^2+x+1\ne0\\x-1\ne0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x\ne1\\\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{3}{4}\ne0\\x\ne1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x\ne0\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ne0\left(luônđúng\right)\end{matrix}\right.\)
\(R=1:\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\)
\(=1:\left(\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right)\)
\(=1:\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=1:\dfrac{x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=1:\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=1:\dfrac{x}{x^2+x+1}\)
\(=\dfrac{x^2+x+1}{x}\)
\(a,R=1:\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\left(x\ne1\right)\\ R=1:\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\\ R=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}=\dfrac{x^2+x+1}{x}=x+1+\dfrac{1}{x}\)
Áp dụng BĐT cosi: \(x+1+\dfrac{1}{x}\ge3\sqrt[3]{x\cdot1\cdot\dfrac{1}{x}}=3\sqrt[3]{1}=3\)
Dấu \("="\Leftrightarrow x=1\)
\(b,\) Áp dụng câu (a), GTNN của A là \(-3\Leftrightarrow x=1\)
\(c,R>4\Leftrightarrow R-4>0\Leftrightarrow x+1+\dfrac{1}{x}-4>0\\ \Leftrightarrow\dfrac{x^2-3x+1}{x}>0\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2-3x+1>0\\x>0\end{matrix}\right.\\\left\{{}\begin{matrix}x^2-3x+1< 0\\x< 0\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< \dfrac{3-\sqrt{5}}{2},x>\dfrac{3+\sqrt{5}}{2}\\x>0\end{matrix}\right.\\\left\{{}\begin{matrix}\dfrac{3-\sqrt{5}}{2}< x< \dfrac{3+\sqrt{5}}{2}\\x< 0\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x< \dfrac{3-\sqrt{5}}{2},x>\dfrac{3+\sqrt{5}}{2}\\x\in\varnothing\end{matrix}\right.\)
\(\Leftrightarrow x< \dfrac{3-\sqrt{5}}{2},x>\dfrac{3+\sqrt{5}}{2}\)
Gòi câu d tự thay dô ik, mỏi tay wa
a: Ta có: \(R=1:\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\)
\(=1:\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x^2-x}\)
\(=\dfrac{x^2+x+1}{x}\)
\(\Leftrightarrow R-3=\dfrac{x^2-2x+1}{x}=\dfrac{\left(x-1\right)^2}{x}>0\forall x\)
Do đó: R>3
d: Thay \(x=\dfrac{1}{4}\) vào R, ta được:
\(R=\left(\dfrac{1}{16}+\dfrac{1}{4}+1\right):\dfrac{1}{4}=\dfrac{21}{4}\)