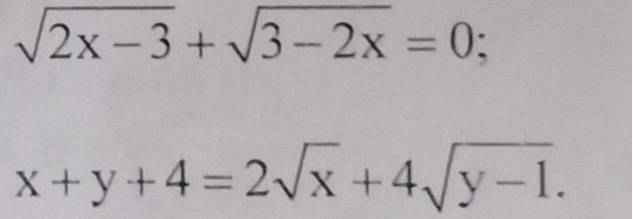ĐKXĐ: \(\left\{{}\begin{matrix}2x-3\ge0\\3-2x\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x\ge\dfrac{3}{2}\end{matrix}\right.\Rightarrow x\ge\dfrac{3}{2}\)
\(\sqrt{2x-3}+\sqrt{3-2x}=0\\ \Rightarrow\left(\sqrt{2x-3}+\sqrt{3-2x}\right)^2=0^2\\ \Rightarrow\left(\sqrt{2x-3}\right)^2+2\sqrt{2x-3}\sqrt{3-2x}+\left(\sqrt{3-2x}\right)^2=0\)
\(\Rightarrow2x-3+\sqrt{4\left(2x-3\right)\left(3-2x\right)}+3-2x=0\)
\(\Rightarrow\sqrt{4\left(2x-3\right)\left(3-2x\right)=0}\)
\(\Rightarrow\sqrt{4.\left[2x\left(3-2x\right)-3.\left(3-2x\right)\right]}=0\)
\(\Rightarrow\sqrt{4.\left(6x-4x^2-9+6x\right)}=0\)
\(\Rightarrow\sqrt{4.\left(12x-4x^2-9\right)}=0\)
\(\Rightarrow\sqrt{48x-16x^2-36}=0\)
\(\Rightarrow48x-16x^2-36=0^2\)
\(\Rightarrow-16x^2+48x-36=0\)
\(\Rightarrow-\left(16x^2-48x+36\right)=0\)
\(\Rightarrow\left(4x-6\right)^2=0\)
\(\Rightarrow4x-6=0\)
\(\Rightarrow x=\dfrac{3}{2}\)
\(\sqrt{2x-3}+\sqrt{3-2x}=0\)
Để phương trình có nghĩa thì 2x - 3 >=0 và 3-2x>=0
=> x =< 3/2 và x >=3/2
=> x = 3/2
Thay x = 3/2 vào pt thỏa mãn
Vậy x=3/2 là nghiệm của phương trình
Phương trình 2 chuyển vế đưa về bình phương dạng:
a^2 + b^2 = 0
<=> a = 0 và b = 0