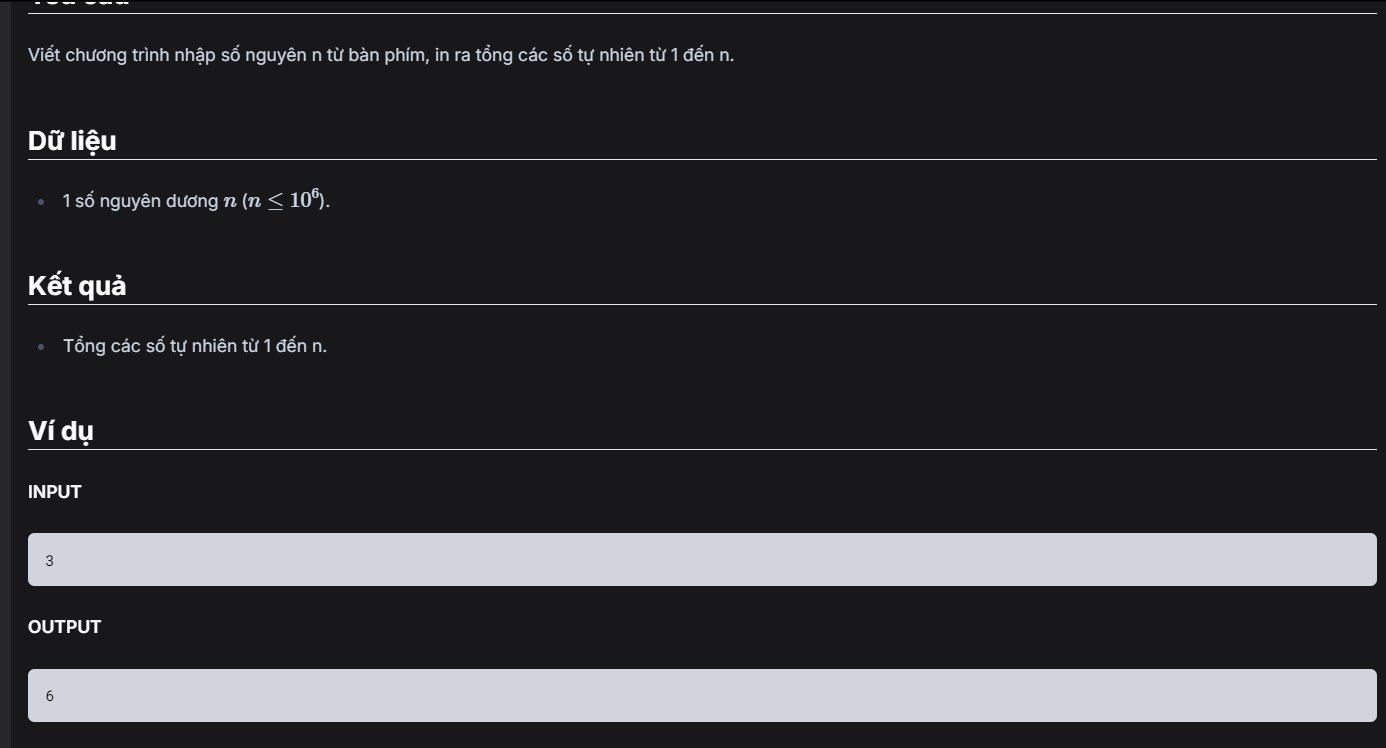
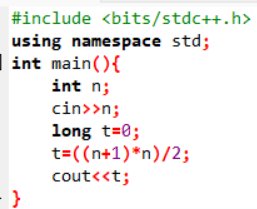
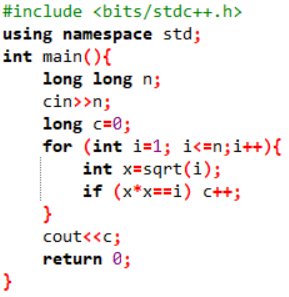
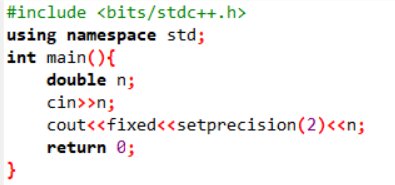
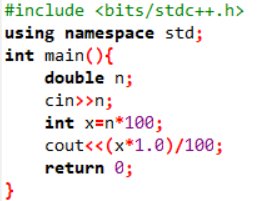
S=2+4+6+...+n trong lập trình C++
viết đầy đủ#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
long long S;
cin >> n;
for (int i = 0; i <= n; i ++)
if (i % 2 == 0) S = S + i;
cout << S;
return 0;
}
Đúng 0
Bình luận (0)
Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính AB, chúng cắt nhau tại M ( M và B nằm khác phía đối với AC). Chứng minh rằng AM // BC
Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
Đúng 0
Bình luận (0)
Xét `ΔAMB` và `ΔCAB`, có:
`AB = CA` (bán kính cung tròn tâm `C`)
`AM = CB` (bán kính cung tròn tâm A)
`BM = BA` (bán kính cung tròn tâm A)
`=> ΔAMB = ΔCAB` (c.c.c)
`=> hat{MAB} = hat{ACB} (hai góc tương ứng)
Mà:
`hat{MAB}` và `hat{MAC}` là hai góc kề bù.
`hat{ACB}` và `hat{BCM}` là hai góc kề bù.
Do đó:
`hat{MAC} = hat{BCM}`
Vì `hat{MAC} = hat{BCM}` (hai góc so le trong bằng nhau) nên:
AM // BC
Đúng 0
Bình luận (0)
đáp án nè cậu
Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
Đúng 0
Bình luận (0)
nhập dãy số a1, a2, ...an hãy lập code để tìm ra các cặp số có tổng bằng K c++
Cho một dãy số gồm 𝑛 phần tử 𝑎1, 𝑎2, … , 𝑎𝑛. Hãy tìm đoạn [a, b] có độ dài ngắn nhất chứa toàn bộ các số trong dãy đã cho? Dữ liệu: • Dòng đầu chứa số nguyên dương 𝑛 (𝑛 ≤ 1000) • Dòng tiếp theo chứa n số nguyên 𝑎1, 𝑎2, … , 𝑎𝑛 |𝑎𝑖 | ≤ 109 Kết quả: Ghi ra hai số a, b là số đầu và cuối của đoạn tìm được. Sử dụng c++.Ví dụ:Sample Input8 5 2 -1 0 1 -3 4 9Sample Output-3 9-------------------------Sample Input4 -1 -3 -5 -7Sample Output-7 -1
Đọc tiếp
Cho một dãy số gồm 𝑛 phần tử 𝑎1, 𝑎2, … , 𝑎𝑛. Hãy tìm đoạn [a, b] có độ dài ngắn nhất chứa toàn bộ các số trong dãy đã cho? Dữ liệu: • Dòng đầu chứa số nguyên dương 𝑛 (𝑛 ≤ 1000) • Dòng tiếp theo chứa n số nguyên 𝑎1, 𝑎2, … , 𝑎𝑛 |𝑎𝑖 | ≤ 109 Kết quả: Ghi ra hai số a, b là số đầu và cuối của đoạn tìm được. Sử dụng c++.
Ví dụ:
Sample Input
8
5 2 -1 0 1 -3 4 9
Sample Output
-3 9
-------------------------
Sample Input
4
-1 -3 -5 -7
Sample Output
-7 -1
Nếu dễ hiểu hơn thì bài toán này sẽ là tìm số nhỏ nhất và số lớn nhất trong mảng. Bởi vì từ số nhỏ nhất đến số lớn nhất nó đã bao gồm tất cả các phần tử đã cho.
Code tham khảo: (bạn tự gõ lại để hiểu hơn về cách mình làm nhé).

Đúng 1
Bình luận (0)
Câu 4. BOI - Bội đặc biệt (3 điểm) Cho trước một số nguyên dương P không chia hết cho 2 và 5. Số X được gọi là một bội đặc biệt của P nếu số X chia hết cho P và X chỉ chứa toàn chữ số 9, Vi dụ: Với P 7 thì X 999999 là một bội đặc biệt của số P. Yêu cầu: Cho trước hai nguyên dương P và N. Hỏi có bao nhiêu số X là bội đặc biệt của P và X có số chữ số không vượt quá N. Dữ liệu vào: Đọc từ file văn bản BOI.INP hai số P và N trên cùng một dòng, mỗi số cách nhau một dấu cách. Dữ liệu ra: Ghi ra file...
Đọc tiếp
Câu 4. BOI - Bội đặc biệt (3 điểm) Cho trước một số nguyên dương P không chia hết cho 2 và 5. Số X được gọi là một bội đặc biệt của P nếu số X chia hết cho P và X chỉ chứa toàn chữ số 9, Vi dụ: Với P = 7 thì X = 999999 là một bội đặc biệt của số P. Yêu cầu: Cho trước hai nguyên dương P và N. Hỏi có bao nhiêu số X là bội đặc biệt của P và X có số chữ số không vượt quá N. Dữ liệu vào: Đọc từ file văn bản BOI.INP hai số P và N trên cùng một dòng, mỗi số cách nhau một dấu cách. Dữ liệu ra: Ghi ra file văn bản BOI.OUT số m là số lượng các số X thỏa mãn yêu cầu. Ví dụ: BOL.INP 77 BOLOUT 1 Giải thích: Với P = 7 và N = 7 ta có duy nhất một số X = 999999 thỏa mãn.
làm bằng pascal mọi người nhé,em cảm ơn!
gp kiếm ở đâu vậy mn
Là bn phải tích cực trl các câu hỏi của giáo viên và học sinh thì dc các thầy cô giáo hoặc CTVIP tick ạ.
Đúng 4
Bình luận (0)
Kiếm ở đâu sao ko hỏi thử ông này ý Kudo Shinichi@![]()
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Câu 2. Chính PhươngCho 2 số nguyên dương A, B (1≤A B ≤ 10¹²). Và người ta định nghĩa số chính phương là bình phương của một số. Ví dụ: 9 là số chính phương vì 9 32.Yêu cầu: Đếm số lượng số chính phương trong đoạn [A, B].Dữ liệu: Vào từ file CP.INP gồm một dòng duy nhất chứa 2 số nguyên dương A và B.Kết quả: Ghi ra file CP.OUT một số nguyên là kết quả của bài toán.Ví dụ:CP.INPCP.OUT241Giới hạn: + Có 30% số điểm có A B; + Có 30% số điểm có B ≤ 106: + Có 40% số điểm có B ≤ 1012.c++ nha. giúp mk
Đọc tiếp
Câu 2. Chính Phương
Cho 2 số nguyên dương A, B (1≤A < B ≤ 10¹²). Và người ta định nghĩa số chính phương là bình phương của một số. Ví dụ: 9 là số chính phương vì 9 = 32.
Yêu cầu: Đếm số lượng số chính phương trong đoạn [A, B].
Dữ liệu: Vào từ file CP.INP gồm một dòng duy nhất chứa 2 số nguyên dương A và B.
Kết quả: Ghi ra file CP.OUT một số nguyên là kết quả của bài toán.
Ví dụ:
CP.INP
CP.OUT
24
1
Giới hạn: + Có 30% số điểm có A = B; + Có 30% số điểm có B ≤ 106: + Có 40% số điểm có B ≤ 1012.
c++ nha. giúp mk
giúp mk bài này với

#include <bits/stdc++.h>
using namespace std;
int main(){
int a,b,c;
cin >>a>>b>>c;
long long s= (long long)a*b-c;
cout<<s;
return 0;
}
Đúng 0
Bình luận (0)
giúp mk với ( lập trình c++)

1/
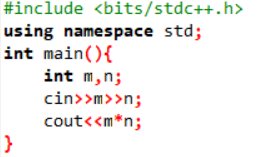
Giải thích:
- Nhà trường có thể chọn 1 nam từ m bạn
- Nhà trường có thể chọn 1 nữ từ n bạn
=> Nhà trường có thể chọn m x n đôi.
2/ Công thức chọn 2 phần tử từ n phần tử là:
\(C\left(n,2\right)=\dfrac{n!}{k!\left(n-2\right)!}\)
Với điều kiện của n như vậy thì sẽ bị tràn á bạn xem lại đề có nhầm gì không nha![]() .
.
Đúng 2
Bình luận (0)