Tập xác định: D = R
y'= -3x2 + 2x
y' = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔ 
Bảng biến thiên:
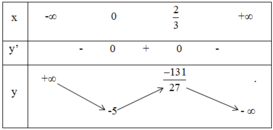
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3).
Tập xác định: D = R
y'= -3x2 + 2x
y' = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔ 
Bảng biến thiên:

Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3).
Xét sự đồng biến, nghịch biến của các hàm số: y = x − sinx, x ∈ [0; 2 π ].
Xét sự đồng biến, nghịch biến của hàm số:
a) y = 4 + 3x – x^2
b) y = x^4 - 2x^2 + 3
c) y = -x^3 + x^2 – 5
Xét sự đồng biến, nghịch biến của các hàm số: y = sin(1/x), (x > 0)
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Xét sự đồng biến, nghịch biến của hàm số:
y = x 4 - 2 x 2 + 3
Xét sự đồng biến, nghịch biến của các hàm số: y = x 4 + 8 x 2 + 5
Xét sự đồng biến, nghịch biến của các hàm số: y = 16x + 2 x 2 − 16 x 3 /3 − x 4
Xét sự đồng biến, nghịch biến của hàm số:
y = 1 3 x 3 + 3 x 2 - 7 x - 2
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
y = (x + 1)/(x - 1) trên đoạn [3; 5].