TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 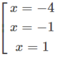
Bảng biến thiên:
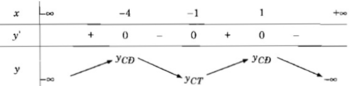
Vậy hàm số y đã cho đồng biến trên các khoảng (- ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 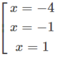
Bảng biến thiên:

Vậy hàm số y đã cho đồng biến trên các khoảng (- ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
Xét sự đồng biến, nghịch biến của các hàm số: y = x − sinx, x ∈ [0; 2 π ].
Xét sự đồng biến, nghịch biến của hàm số:
a) y = 4 + 3x – x^2
b) y = x^4 - 2x^2 + 3
c) y = -x^3 + x^2 – 5
Xét sự đồng biến, nghịch biến của các hàm số: y = sin(1/x), (x > 0)
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV. m i n x ∈ R g ( x ) = f ( 9 )
A. 1
B. 2
C. 3
D. 4
tìm khoảng đồng biến nghịch biến của hàm số sau
a) y = \(-x^4\) + \(8x^2\) + 1
b) y = \(x^4\) - 3
Xét sự đồng biến, nghịch biến của hàm số:
y = x 4 - 2 x 2 + 3
Xét sự đồng biến, nghịch biến của hàm số:
y = 1 3 x 3 + 3 x 2 - 7 x - 2