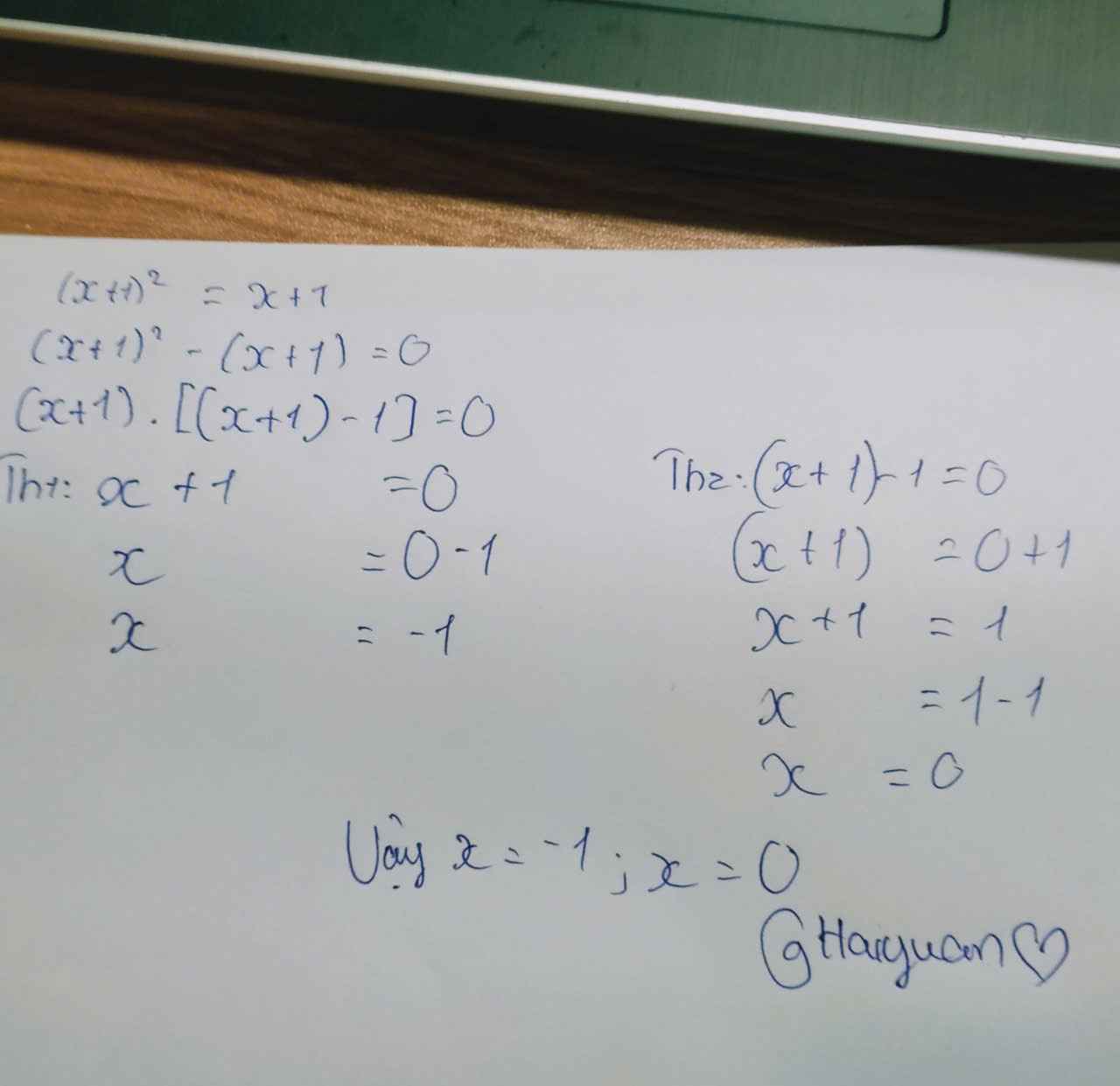Question

(x+1)mũ 2=x+1

 

Answer 1

`(x + 1)^2 = x +  1`

`=> (x + 1)^2 - (x + 1)= 0`

`=> (x + 1)[(x + 1)- 1] = 0`

`=> (x + 1).x=0`

`=> [(x + 1 = 0),(x = 0):}`

`=> [(x = -1),(x = 0):}`

Vậy: `x = -1; x=0`

Answer 2

\(\left(x+1\right)^2=x+1\)

=>\(\left(x+1\right)^2-\left(x+1\right)=0\)

=>(x+1)(x+1-1)=0

=>x(x+1)=0

=>\(\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

Answer 3

` x + 1 = 0 ` 
\[ => 
x = -1
\]
\[
(-1 + 1)^2 = -1 + 1
\]
\[
0 = 0
\]
Vậy \( x = -1 \) là một nghiệm của phương trình.
\[
\frac{(x + 1)^2}{x + 1} = \frac{x + 1}{x + 1}
\]
\[
x + 1 = 1
\]
\[
x = 0
\]

Answer 4