=>3x+9y+6z=3 và 10x-2y+6z=32 và -18x+42y+6z=-84
=>-7x+11y=-29 và 21x-33y=87 và x+3y+2z=1
=>\(\left(x,y,z\right)\in R\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
21 tháng 6 2021 lúc 22:10
Cho x,y,z là các số thực dương thỏa mãn \(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=12\)
Tìm GTLN của biểu thức \(P=\frac{1}{2x+3y+3z}+\frac{1}{3x+2y+3z}+\frac{1}{3x+3y+2z}\)
Hệ phương trình
2
x
-
5
y
+
z
10
x
+
2
y
-
3
z...
Đọc tiếp
Hệ phương trình 2 x - 5 y + z = 10 x + 2 y - 3 z = 10 - x + 3 y + 2 z = - 16 có nghiệm là:
A. 2 ; - 2
B. - 2 ; 2 ; 4
C. 2 ; - 2 ; - 4
D. 2 ; - 1 ; 1
Cho x,y,z>0
\(CM:\sqrt{\dfrac{x}{z+3x}}+\sqrt{\dfrac{y}{x+3y}}+\sqrt{\dfrac{z}{y+3z}}\le\dfrac{3}{2}\)
Giải hệ phương trình
2
x
-
3
y
+
z
-
7...
Đọc tiếp
Giải hệ phương trình 2 x - 3 y + z = - 7 - 4 x + 5 y + 3 z = 6 x + 2 y - 2 z = 5
7 tháng 1 2022 lúc 13:08
Giải hệ phương trình sau(giải chi tiết)
\(\hept{\begin{cases}x+3y+2z=8\\2x+2y+z=6\\3x+y+z=6\end{cases}}\)
cho x,y,z là các số thực dương tm \(3xyz\ge x+y+z\)
tìm min của P= \(\frac{xy+yz+xz-1}{\sqrt{3x^2+1}+\sqrt{3y^2+1}+\sqrt{3z^2+1}}\)
Cho hệ phương trình
-
x
+
2
y
-
3
z
2
6
x
-
y
+...
Đọc tiếp
Cho hệ phương trình - x + 2 y - 3 z = 2 6 x - y + 3 z = - 3 - 2 x - 3 y + z = 2
Giả sử (x; y;z) là nghiệm của hệ phương trình. Trong các khẳng định sau, khẳng định đúng là
Giải các hệ phương trình
x
+
3
y
+
2
z
8
2...
Đọc tiếp
Giải các hệ phương trình x + 3 y + 2 z = 8 2 x + 2 y + z = 6 3 x + y + z = 6
Cho hệ phương trình
2
x
-
3
y
+
4
z
-
5
-
4
x
+...
Đọc tiếp
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
Giải các hệ phương trình
x
-
3
y
+
2
x
-
7...
Đọc tiếp
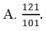
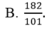
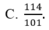
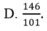
Giải các hệ phương trình x - 3 y + 2 x = - 7 - 2 x + 4 y + 3 z = 8 3 x + y - z = 5