Các câu hỏi tương tự
Với giá trị nào của m thì hàm số
y
sin
x
-
m
sin
x
+
m
đồng biến trên khoảng
0
;
π
2
? A. m 0 B.
-
1
≤
m
0
C. -1 m 0 D. -1...
Đọc tiếp
Với giá trị nào của m thì hàm số y = sin x - m sin x + m đồng biến trên khoảng 0 ; π 2 ?
A. m > 0
B. - 1 ≤ m < 0
C. -1 < m < 0
D. -1 < m
Tìm tất cả các giá trị thực của tham số m để hàm số
y
sinx
−
m
sinx
+
m
đồng biến trong khoảng
0
;
π
2
. A.
m
≥
0
B.
m
0
C. ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = sinx − m sinx + m đồng biến trong khoảng 0 ; π 2 .
A. m ≥ 0
B. m > 0
C. − ∞ ; − 1 ∪ 0 ; + ∞
D. − ∞ ; − 1 ∪ 0 ; + ∞
Tìm tất cả các giá tri thưc của tham số m sao cho hàm số
y
s
inx
−
1
s
inx
−
m
đồng biến trên khoảng
0
;
π
2
. A. m 1 B.
m
≤
0
C. m 0 hoặc ...
Đọc tiếp
Tìm tất cả các giá tri thưc của tham số m sao cho hàm số y = s inx − 1 s inx − m đồng biến trên khoảng 0 ; π 2 .
A. m < 1
B. m ≤ 0
C. m < 0 hoặc m ≥ 1
D. 0 ≤ m ≤ 1
Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
s
inx+
cos
2
x
+
sin
3
x
trên đoạn
0
;
π
. Tính P M + m A.
P
16
27
B.
P
−
19
+
13...
Đọc tiếp
Gọi M , m theo thứ tự là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = s inx+ cos 2 x + sin 3 x trên đoạn 0 ; π . Tính P = M + m
A. P = 16 27
B. P = − 19 + 13 13 27
C. P = − 19 − 13 13 27
D. P = − 16 27
Với giá trị nào của tham số m thì hàm số
y
x
3
-
6
x
2
+
m
x
+
1
đồng biến trên khoảng
0
;
+
∞...
Đọc tiếp
Với giá trị nào của tham số m thì hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng 0 ; + ∞ ?
A. m ≥ 0
B. m ≤ 0
C. m ≥ 12
D. m ≤ 12
Tìm tất cả các giá trị thực của m để hàm số
y
(
m
2
+
m
+
1
)
x
+
(
m
2
-
m
+
1
)
sin
x
luôn đồng biến trên
(
0
;
2
π
)
A.
m
≤
0
B.
m
≥
0
C.
m
0
D.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của m để hàm số y = ( m 2 + m + 1 ) x + ( m 2 - m + 1 ) sin x luôn đồng biến trên ( 0 ; 2 π )
A. m ≤ 0
B. m ≥ 0
C. m > 0
D. m < 0
Cho hàm số y f (x) liên tục trên
ℝ
và có đồ thị như hình vẽ bên.Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) m có nghiệm thuộc khoảng (0;
π
) là A. [-1;3) B. (-1;1) C. (-1;3) D. [-1;1 )
Đọc tiếp
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
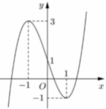
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)m có nghiệm thuộc khoảng
0
;
π
là A. (-1;3) B. (-1;1) C. (-1;3) D. (-1;1)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)=m có nghiệm thuộc khoảng 0 ; π là
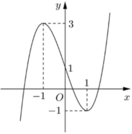
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Với giá trị nào của m thì hàm số
y
tan
x
-
2
m
tan
x
-
2
đồng biến trên khoảng
0
;
π
4
? A.
1
m
≤
2
B. ...
Đọc tiếp
Với giá trị nào của m thì hàm số y = tan x - 2 m tan x - 2 đồng biến trên khoảng 0 ; π 4 ?
A. 1 < m ≤ 2
B. - ∞ ; 2
C. 1 < m < 2
D. 2 ; + ∞




