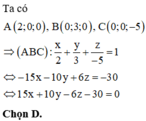Các câu hỏi tương tự
Viết phương trình tổng quát của mặt phẳng (α) qua ba điểm A, B, C lần lượt là hình chiếu của điểm M(2;3;-5) xuống các trục Ox, Oy, Oz A. 15x - 10y - 6z - 30 0 B. 15x - 10y - 6z + 30 0 C. 15x + 10y - 6z + 30 0 D. 15x + 10y - 6z - 30 0
Đọc tiếp
Viết phương trình tổng quát của mặt phẳng (α) qua ba điểm A, B, C lần lượt là hình chiếu của điểm M(2;3;-5) xuống các trục Ox, Oy, Oz
A. 15x - 10y - 6z - 30 = 0
B. 15x - 10y - 6z + 30 = 0
C. 15x + 10y - 6z + 30 = 0
D. 15x + 10y - 6z - 30 = 0
Trong không gian với hệ toạ độ Oxyz, cho hình lập phương giới hạn bởi các mặt phẳng x0;y0;z0;x10;y10;z10. Gọi S là tập hợp tất cả các điểm A(x;y;z),(
x
,
y
,
z
∈
Z
) nằm bên trong (kể cả các mặt) của hình lập phương. Lấy ngẫu nhiên một điểm A(x;y;z)
∈
S. Xác suất để xy và xz bằng A.
285
1331
B.
35
121
C.
20...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hình lập phương giới hạn bởi các mặt phẳng x=0;y=0;z=0;x=10;y=10;z=10. Gọi S là tập hợp tất cả các điểm A(x;y;z),( x , y , z ∈ Z ) nằm bên trong (kể cả các mặt) của hình lập phương. Lấy ngẫu nhiên một điểm A(x;y;z) ∈ S. Xác suất để x<y và x<z bằng
A. 285 1331
B. 35 121
C. 204 1331
D. 57 200
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
(
α
)
:
bc
.
x
+
ac
.
y
+
ab
.
z
-
abc
0
với a, b, c là các số khác 0 thỏa mãn
1
a
+
2
b
+
3
c
7
. Gọi A, B, C lần lượt là giao điểm củ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( α ) : bc . x + ac . y + ab . z - abc = 0 với a, b, c là các số khác 0 thỏa mãn 1 a + 2 b + 3 c = 7 . Gọi A, B, C lần lượt là giao điểm của α với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng α tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 72 7 . Thể tích khối OABC với O là gốc tọa độ bằng
A. 2 9
B. 3 4
C. 1 8
D. 4 3
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2) Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x Ox, y Oy, z Oz lần lượt tại các điểm A, B, C sao cho
O
A
O
B
O
C
≠
0
?
A. 3 B. 1 C. 4 D. 8
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2) Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x Ox, y Oy, z Oz lần lượt tại các điểm A, B, C sao cho O A = O B = O C ≠ 0 ?
A. 3
B. 1
C. 4
D. 8
Trong không gian Oxyz, cho mặt cầu (S):
x
-
1
2
+
y
-
2
2
+
z
-
1
2
6
tiếp xúc với hai mặt phẳng
P
:
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y - 2 2 + z - 1 2 = 6 tiếp xúc với hai mặt phẳng P : x + y + 2 z + 5 = 0 , Q : 2 x - y + z - 5 = 0 lần lượt tại các điểm A, B. Độ dài đoạn AB là
A. 3 2
B. 3
C. 2 6
D. 2 3
Trong không gian với hệ toạ độ Oxyz, cho điểm A(-3;-1;3) và đường thẳng d:
x
-
1
3
y
-
1
2
z
-
5
2
, mặt phẳng (P):x+2y-z+50. Đường thẳng
Δ
qua A và cắt d tại điểm B(a;b;c) và tạo với mặt phẳng (P) góc...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm A(-3;-1;3) và đường thẳng d: x - 1 3 = y - 1 2 = z - 5 2 , mặt phẳng (P):x+2y-z+5=0. Đường thẳng Δ qua A và cắt d tại điểm B(a;b;c) và tạo với mặt phẳng (P) góc 30 ° . Tính T=a+b+c.
A. T = 14
B. T = 0
C. T = 21
D. T = 7
Trong không gian với hệ trục Oxyz cho hai điểm
A
1
;
2
;
1
, B
3
;
0
;
-
1
và mặt phẳng (P) có phương trình
x
+
y
−
z
0.
Gọi M và N lần lượt là hình chiếu của A và B trên mặt phẳn...
Đọc tiếp
Trong không gian với hệ trục Oxyz cho hai điểm A 1 ; 2 ; 1 , B 3 ; 0 ; - 1 và mặt phẳng (P) có phương trình x + y − z = 0. Gọi M và N lần lượt là hình chiếu của A và B trên mặt phẳng (P). Tính độ dài đoạn MN
A. 2 3
B. 4 2 3
C. 2 3
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-
2
1
,
d
:
x
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng ∆ thay đổi trên (P) nhưng luôn đi qua H đồng thời ∆ cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính T= a+b
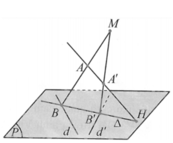
A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
2
y
-
2
1
z
+
1
3
và mặt phẳng
P
:
x
+
y
+
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x - 1 2 = y - 2 1 = z + 1 3 và mặt phẳng P : x + y + z - 3 = 0 . Đường thẳng d ' là hình chiếu của d theo phương Ox lên (P), d ' nhận u → a ; b ; 2019 làm một véc tơ chỉ phương. Xác định tổng a + b
A. 2019
B. - 2019
C. 2018
D. - 2020