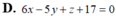a: Gọi (d) là đường thẳng đi qua B(1;-1;3) và song song với giá của mỗi vecto \(\overrightarrow{u}=\left(2;0;-3\right);\overrightarrow{v}=\left(4;3;-1\right)\)
Gọi \(\overrightarrow{a}=\left\lbrack\overrightarrow{u};\overrightarrow{v}\right\rbrack\)
Tọa độ của \(\overrightarrow{a}\) là:
\(\begin{cases}x=0\cdot\left(-1\right)-\left(-3\right)\cdot3=-1+9=8\\ y=-3\cdot4-2\cdot\left(-1\right)=-12+2=-10\\ z=2\cdot3-0\cdot4=6\end{cases}\)
Phương trình chính tắc của (d) là:
\(\frac{x-1}{8}=\frac{y-\left(-1\right)}{-10}=\frac{z-3}{6}\)
=>\(\frac{x-1}{8}=\frac{y+1}{-10}=\frac{z-3}{6}\)
Phương trình tham số của (d) là:
\(\begin{cases}x=1+8t\\ y=-1-10t\\ z=3+6t\end{cases}\)
b: A(1;2;0); B(4;3;2)
\(\overrightarrow{AB}=\left(4-1;3-2;2-0\right)=\left(3;1;2\right)\)
Gọi (d) là phương trình đường thẳng đi qua hai điểm A(1;2;0); B(4;3;2) và vuông góc với mặt phẳng (β): 2x-5y+z-9=0
(β): 2x-5y+z-9=0
=>Vecto chỉ phương là \(\overrightarrow{a}\) =(2;-5;1)
Đặt \(\overrightarrow{b}=\left\lbrack\overrightarrow{AB};\overrightarrow{a}\right\rbrack\)
Tọa độ của \(\overrightarrow{b}\) là:
\(\begin{cases}x=1\cdot1-2\cdot\left(-5\right)=1+10=11\\ y=2\cdot2-3\cdot1=4-3=1\\ z=3\cdot\left(-5\right)-1\cdot2=-15-2=-17\end{cases}\)
=>(d) đi qua A(1;2;0) và nhận \(\overrightarrow{b}\) =(11;1;-17) làm vecto chỉ phương
Phương trình chính tắc của (d) là:
\(\frac{x-1}{11}=\frac{y-2}{1}=\frac{z-0}{-17}\)
=>\(\frac{x-1}{11}=\frac{y-2}{1}=\frac{z}{-17}\)
Phương trình tham số của (d) là:
\(\begin{cases}x=1+11t\\ y=2+t\\ z=0+\left(-17\right)t=-17t\end{cases}\)