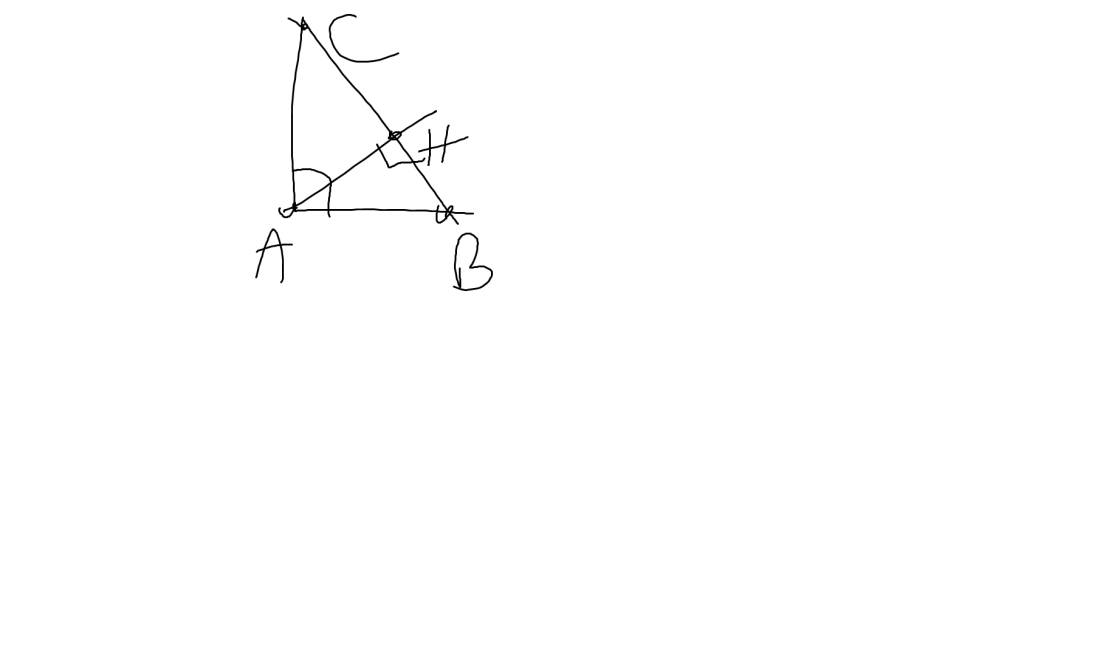
a: Ta có: \(\widehat{HAB}+\widehat{B}=90^0\)(ΔHAB vuông tại H)
\(\widehat{C}+\widehat{B}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{HAB}=\widehat{C}\)
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔHBA~ΔHAC
c: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{HB}{AB}=\dfrac{AB}{BC}=\dfrac{HA}{AC}\)
=>\(\dfrac{HB}{3}=\dfrac{3}{5}=\dfrac{HA}{4}\)
=>\(HB=3\cdot\dfrac{3}{5}=1,8\left(cm\right);HA=3\cdot\dfrac{4}{5}=2,4\left(cm\right)\)
HB+HC=BC
=>HC+1,8=5
=>HC=3,2(cm)
Đúng 1
Bình luận (0)
